Set Theory
Reference:
- UIUC math432 Set Theory and Topology by Prof. Roy Araiza.
- Set Theory and Metric Spaces by Irving Kaplansky.
1. Basic Set Theory
1.1. Basic Operations on Sets
\(A\) is properly included in \(B\), denoted by \(A \subsetneq B\), if \(A \subset B\) and \(A \neq B\).
1.2. Partially Order Sets
Let \(L\) be a set and \(\preceq\) be an order (\(\cdot \preceq \cdot : L \times L \to \{ \mTRUE, \mFALSE \}\)). We say \((L, \preceq)\) is a partially ordered set (poset) if
- Reflectivity: \(\forall a \in L, a \preceq a\),
- Transitivity: If \(a \preceq b\) and \(b \preceq c\), then \(a \preceq c\).
- Anti-symmetry: If \(a \preceq b\) and \(b \preceq a\), then \(a = b\) (meaning that \(a\) and \(b\) are the same element),
If \(a \preceq b\) and \(a \neq b\) we write \(a < b\).
To show that a given \((L, \preceq)\) is a poset, we may prove transitivity and then anti-symmetry, because we can deduce \(a \preceq b, b \preceq a \implies a \preceq a\) from transitivity, which gives one more condition.
A chain is a partially ordered set in which, for any \(a\) and \(b\), either \(a \preceq b\) or \(b \preceq a\).
Let \(S\) be a subset of a poset \(L\). An element \(u \in L\) (not necessarily in \(s\)) is called
- an upper bound of \(S\) if \(s \preceq u\) for all \(s \in S\),
- a least upper bound (or supremum) \(S\) if \(s \preceq \) any upper bound of \(S\).
Lower bound and greatest lower bound (or infimum)are defined analogously.
Properties:
- If a supremum (or an infimum) exists, then it is unique (by \(\preceq\)). Thus, it is safe to define (“the”) \(\sup S, \inf S\) (if they exist).
- The existence is not guaranteed (e.g., \(S = L\)).
An element \(u\) of a partially ordered set \(L\) is a top element of \(L\) if \(a \preceq u\) for all \(a \in L\). Bottom element is defiend analogously.
Properties:
- The existence is not guaranteed (paritially ordered)
Given a poset \((L, \preceq)\), if all nonempty subsets of \(L\) have a top element and bottom element, then \(L\) must be a finite chain.
\(L\) is a chain: For any two elements \(a, b\) in \(L\), consider the subset \(\{ a, b \} \subseteq L\).
\(L\) is finite: \(L\) has a top element \(t_0\) and a bottom element \(b_0\). If \(L \setminus \{ t_0, b_0 \} \neq \emptyset\) , then it also has a top element \(t_1\) and a bottom element \(b_1\), and so on. Suppose \(L\) is infinite, then the process goes forever and we have an infinite chain \(b_0 \preceq b_1 \preceq \dots \) (similar for top elements) that does not have a top element, which is a contradiction.
Let \(L\) be a poset.
- \(u \in L\) is a maximal element if \(u \prec l\) is NOT true for all \(l \in L\). Equivalently, if the only \(\hat{u} \in L\) s.t. \(u \preceq \hat{u}\) is \(u\) itself.
- \(u \in L\) is a minimal element if \(u \succ l\) is NOT true for all \(l \in L\). Equivalently, if the only \(\hat{u} \in L\) s.t. \(u \succeq \hat{u}\) is \(u\) itself.
P.S.: for maximal element, it does not necessarily imply that \(u \succeq l\) is true because there might not be an ordering (\(L\) may not be a chain).
1.3. Lattices
A lattice is a poset in which (the set of) every two elements have a supremum and an infimum (again, not necessarily in the set). \(a \vee b\) denotes the supremum and \(a \wedge b\) denotes the infimum.
- A lattice is complete if any subset of it has a supremum and an infimum.
- A lattice is distributive if \(a \wedge (b \vee c) = (a \wedge b) \vee (a \wedge c)\) and \(a \vee (b \wedge c) = (a \vee b) \wedge (a \vee c)\).
- Let \(L\) be a lattice possessing a top element and a bottom element, denoted by \(1\) and \(0\). \(L\) is complemented if for any \(a \in L\), \(\exists b \in L\) s.t. \(a \wedge b = 0\) and \(a \vee b = 1\).
Properties:
- In a lattice any finite subset (denoted by \(S \subset \subset L\)) has a supremum and an infimum: Repeatedly taking \(\vee\) / \(\wedge\) for finitely many times.
- Chains are lattices.
If \(L\) is a lattice in which every chain has a supremum and an infimum, then \(L\) is complete.
1.4. Relations, Cartesian Products, Equivalent Classes
An ordered pair is a tuple. Two ordered pairs \((a, b)\) and \((c, d)\) are equal iff \(a = c\) and \(b = d\).
The Cartesian product of \(A\) and \(B\) is the set of all ordered pairs \((a, b)\) with \(a \in A\) and \(b \in B\), denoted by \(A \times B\).
We can regard a Cartesian product as a function/array: Let \(I\) be an index set, and for each \(i \in I\) let a set \(A_{i}\) be given. Then the cartesian product \(\prod_{i} A_{I}\) is the set of all possible arrays \(\{ a_{i} \}\) with \(a_{i} \in A_{i}\), or the set of all functions \(f: I \to \cup _{i} A_{i}\) satisfying \(f(i) \in A_{i}\).
A relation between sets \(A\) aand \(B\) is a set of ordered pairs \((a, b)\) with \(a \in A\) and \(b \in B\). It is simply a subset of \(A \times B\).
Let \(A\) be a set and let a relation \(\sim\) be given on \(A\) (\(\subset A \times A\)). We denote \(a \sim b\) if \((a, b) \in \sim\). We say that \(\sim\) is an equivalence relation if the following three properties hold:
- Reflexivity: For all \(a\), \(a \sim a\).
- Symmetry: \(a \sim b\) implies \(b \sim a\).
- Transitivity: \(a \sim b\) and \(b \sim a\) implies \(a \sim c\).
Given a set \(A\) and an equivalence relation \(\sim\) on \(A\), the equivalent class of an element \(a \in A\) is defined as \(\bar{a} = \{ x \in X: a \sim x \}\).
A partition of a non-empty set \(X\) is a collection \(\mathcal{A}\) of subsets of \(X\) s.t.
- Each \(A \in \mathcal{A}\) is non-empty.
- Sets in \(\mathcal{A}\) are mutually disjoint.
- \(\cup _{A \in \mathcal{A}} A = X\).
Let \(X\) be a non-empty set and \(\sim\) be an equivalence relation on \(X\). Then, for any \(x, y \in X\), \(\bar{x} \cap \bar{y} \neq \emptyset \implies \bar{x} = \bar{y}\).
Proof: By transitivity.
Let \(X\) be a non-empty set and \(\sim\) be an equivalence relation on \(X\). Then \(\{ \bar{x}: x \in X \}\) is a partition of \(X\).
Conversely, given a partition \(\mathcal{A}\) of \(X\), we may define \(x \sim y\) iff \(x, y \in A\) for some \(A \in \mathcal{A}\). Then \(\sim\) is an equivalence relation on \(X\).
Non-emptiness: Every equivalent \(\bar{x}\) at least contains \(x\). Disjointness: By the previous lemma. Union: easy.
Converse: easy.
1.5. Equivalence and Sets
Let \(\mathcal{A}\) be a collection of sets. Define a relation \(\cong\) on \(\mathcal{A}\) as follows: For any \(A, B \in \mathcal{A}\), \(A \cong B\) iff there exists a bijection from \(A\) to \(B\). Then \(\cong\) is an equivalence relation on \(\mathcal{A}\).
Reflexivity: Identity. Symmetry: Inverse. Transitivity: Composition.
We say two sets \(A\) and \(B\) are equivalent if \(A \cong B\) (defined above).
A set \(S\) is finite iff \(S = \emptyset\) or \(S \cong \{ 1, 2, \dots , n \}\) for some \(n \in \mathbb{N} \). Otherwise, we say \(S\) is infinite.
1.6. Countability
\(\mathbb{Z} \cong \mathbb{N} \).
\(f(x) = 2x\) for \(x > 0\) and \(-(1 + 2x)\) for \(x \leq 0\).
A set is countably infinite iff there exists a bijection from \(A\) to \(\mathbb{N} \). A set is countable if it is either finite or ountablt infinite. Otherwise, it is uncountable.
A countable union of countable sets is countable.
Let \(A = U_{i \in I} A_{i}\), where \(A_{i}\) and \(I\) are countable. Suppose \(I\) is countably infinite, we can reindex the union using \(\mathbb{N} \), i.e., \(A = \cup _{i=1} ^{\infty} A_{n}\). Since each \(A_{n}\) is countable, it can be expresssed as \(A_{n} = \{ A_{n m} \}_{m=1} ^{\infty}\). Then, we can enumerate the union as \(A = \{ a_{11}, a_{12}, a_{21}, a_{31}, a_{22}, \dots \}\). In case there are duplicates, we discard all but the first occurrence.
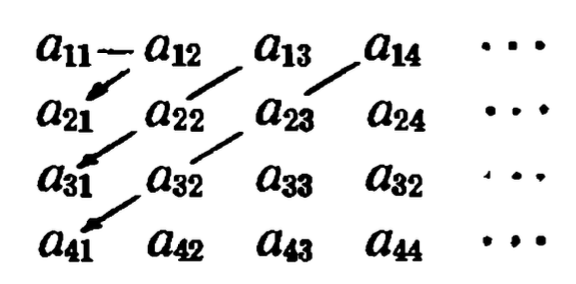
\(\mathbb{Q} \) is countable.
Find a countable union of countable set to express \(\mathbb{Q} \). E.g., \(\mathbb{Q} = \cup _{n=1}^{\infty} \{ \frac{m}{n} | m \in \mathbb{Z} \}\).
An algebraic number is a root of a non-zero polynomial in one variable with rational (equivalently, integer) coefficients.
The set of all algebraic numbers is countable.
Basic idea: write the target set as countable union of countable sets.
Let \(S = \{ f(x): \sum_{k=1}^{n} a_{k} x ^{k}, a_{k} \in \mathbb{Z}, \text{ some } a_{k} \neq 0\) be the set of all such polynomials. Let \(T\) be the set of all algebraic numbers.
For each \(f \in S\), denote by \(T(f) = \{ c \in \mathbb{R} : f(c) = 0 \}\) the set of roots of \(f\). Let \(S_{n} = \{ f \in S: \deg (f) = n \}\). Then, \(S = \cup _{n=1} ^{\infty} S_{n}\). Let \(S_{n, l} = \{ f \in S_{n}: \| f \| \gets l\}\), where \(\| f \| = \sum_{k=1}^{n} \| a_{k} \|\). Then for any finite \(n, l\), \(S_{n, l}\) is finite. And we have \(S_{n} = \cup _{l=1} ^{\infty} S_{n, l}\).
Thus, \(S_{n}\) is countable. And \(S\) is countable. Finally, \(T = \cup _{f \in S} T(f)\) is countable.
A real number is called transcendental if it is not algebraic.
\(\mathbb{R} \) is uncountable.
First prove that the subset \(S\) of real numbers between \(0\) and \(1\) is uncountable. Then, as the supset, \(\mathbb{R} \) is also uncountable.
Suppose \(S\) is countable, i.e., \(S = \{ a_{n} \}_{n=1} ^{\infty}\). We claim that there exists \(b \in S\) s.t. \(b\) does not appear in this enumeration.
Consider expressing numbers in \(S\) using infinite decimals. For the special cases where a decimal ending with infinite 9’s equals to a decimal ending with infinite 0’s, we always take the latter one. Now, for any \(n\), set the \(n\)-th digit of \(b\) to 1 if the \(n\)-th digit of the decimal expression of \(a_{n}\) is 0, and to 0 otherwise. Then, \(b \neq a_{n}\) for all \(n\).
2. Cardinal Numbers
The cardinal number of a set \(o(\cdot )\) is defined as follows: Let \(X, Y\) be two sets. Define
- \(o(X) = o(Y)\) if \(\exists f:X \to Y\), \(f\) is bijective.
- \(o(X) \preceq o(Y)\) if \(\exists f:X \to Y\), \(f\) is injective.
- \(\prec\) if \(\preceq\) but not \(=\).
- \(o(X) \succeq o(Y)\) if \(\exists f:X \to Y\), \(f\) is surjective.
- \(\succ\) if \(\succeq\) but not \(=\).
We denote \(o(\mathbb{N} ) = \aleph_{0}\) (aleph-nought) and \(o(\mathbb{R} ) = c\) (continuum).
Properties:
- The relation \(\preceq\) on cardinal numbers satisfies reflexivity and transitivity.
- Antisymmetry (\(\preceq \land \succeq \implies =\)) is unclear at this point.
- \(\prec\) and \(\succ\) are exclusive.
We say a cardinal number is infinite if it is the cardinal number of a infinite set. By analogy, we have zero (corresponding to \(\emptyset\)), finite, uncountable cardinals, etc.
2.1. Cardinal Numbers of Power Sets
Given any set \(A\), there doesn’t exist a mapping of \(A\) onto \(\mathcal{P}(A)\), but there is an injective mapping of \(A\) into \(\mathcal{P}(A)\). As a result, \(o(A) \neq o(\mathcal{P}(A))\) and \(o(A) \prec o(\mathcal{P}(A))\).
\(\star\) Suppose a sujective map \(f: A \to \mathcal{P}(A)\) exist, we want to show the contradiction that \(\exists B \in \mathcal{P}(A), \nexists b \in A, f(b) = B\).
A tricky construction (by Cantor): Let \(B = \{ a \in A : a \notin f(A) \}\). This basically divides \(A\) into two categories, those map to a set including themselves and those do not. One can verify \(B\) is a valid choice.
How to think of this construction? Think of this weaker condition: \(B\) is a set such that (1) every \(f(b)\), where \(b \in A\), just covers a proper (strict) subset of \(B\), and (2) the covers form a partition of \(B\). Then, considering any \(C \in \mathcal{P}(A)\), we can find that \(\{ c \in C: f(c) = C \}\) (pretending \(A\) is “larger” than \(\mathcal{P}(A)\)) forms a partition of \(B\).
An evident injective map \(g: A \to \mathcal{P}(A)\): For any \(a\), \(g(a) = \{ a \}\).
For any set \(A\), if \(o(A) = d\), then we assign \(o(\mathcal{P}(A)) = 2 ^{d}\).
Let \(d\) be a cardinal number, then \[ d < 2 ^{d} < 2 ^{2 ^{d}} < \dots \] This is the same as the transitivity for the relation \(\prec\) on cardinal numbers of power sets.
Firstly, applying the previous theorem to \(2 ^{d}\) and so on, we have \(2 ^{d} < 2 ^{2 ^{d}}\). By \(\prec \implies \preceq\) and the transitivity of \(\preceq\), this implies \(d_{i} \preceq d_{j}\) for any \(i < j\).
Then, we want to rule out \(d_{i} = d_{j}\). Suppose \(d_{i} = d_{j} = 2 ^{d_{j-1}}\), then we have \(d_{j-1} < 2 ^{d_{j-1}} = d_{i}\). Thus, it suffices to prove \(d_{i} < d_{j-1}\). This can be done inductively.
2.2. TODO Comparison of Cardinal Numbers
Let \(f\) be an injective map of a set \(A\) into itself. Let \(C\) be a subset of \(A\) containing \(f(A)\). Then there exists a bijection between \(A\) and \(C\).
P.S.: Before looking forward, the condition \(f(A) \subset C \subset A\) is just to limit the range of \(f\).
Consider applying \(f\) and \(f ^{-1}\) (if possible) to elements in \(A\) repeatedly.
First, let’s look at the case where \(A\) is finite: Starting from any \(a \in A\), we obtain a sequence \(a, f(a), f(f(a)), \dots \). By injectivity, it is easy to show that it eventually goes back to \(a\) after a finite number of steps (i.e., \(f ^{n}(a) = a\)). This is called a cycle. If we keep doing with starting with an unseen element, we can get disjoint cycles covering \(f(A)\) (but not necessarily \(A\)).
Now, broaden the context to infinite \(A\): For any \(a \in A\), there are several cases:
- If \(a \in f(A)\): Apply \(f\) and \(f ^{-1}\) (if possible) repeatedly to get \(\dots , f ^{-1}(f ^{-1}(a)), f ^{-1}(a), a, f(a), f (f(a)), \dots \)
- If the applications in both direction can go forever without any repetition, then this is called a bilateral infinite cycle.
- If there is ever a repetition, it boils down to a finite cycle.
- If we cannot no longer apply \(f ^{-}\), then this becomes the following case:
- If \(a \notin f(A)\): Could apply \(f\) repeatedly but not \(f ^{-1}\) to get \(a, f(a), f(f(a)), \dots \).
- If it goes forever without any repetition, then it is called a unilateral infinite cycle.
- Actually, there must not be a repetition (if any, the first must be \(a\)), because this violates \(a \notin f(A)\).
Clearly, \(A\) is partitioned into disjoint finite cycles, bilateral cycles, and unilateral cycles. Let’s denote by \(D\) (the set of elements in) all the finite cycles and bilateral infinite cycles and by \(E\) all the unilateral infinite cycles. Then, \(A = D \sqcup E\) and \(f(A) = f(D) \sqcup f(E) = D \sqcup (E \setminus \text{the initial elements})\).
Then, construct a bijection \(g: A \to C\): We consider assign values by cycles. If we use \(f\) on some subset of \(A\), we don’t need to worry about the injectivity of that part. However, we have to cover entire \(C\).
- For unilateral cycle with an initial element \(\in C\): Better not to set \(g = f\), because the initial element \(\in C\) is not mapped to. We set \(g = \) the identity map.
- For unilateral cycle with an initial element \(\notin C\): Set \(g = f\).
- For \(D\): Any bijection between \(D\) and \(D\). E.g., the identity map or \(f\) (rigorous verification needed).
It can be easily checked that \(g\) is bijective.
Let \(A\) and \(B\) be sets s.t. there exists an injective map of \(A\) into \(B\) (\(o(A) \preceq o(B)\)) and an injective map of \(B\) into \(A\) (\(o(B) \preceq o(A)\)). Then there exists a bijection between \(A\) and \(B\).
In other words, the relation \(\preceq\) on cardinal numbers is antisymmetric and hence a partial ordering.
Let \(L\) be a poset in which every chain has an upper bound. Then \(L\) contains a maximal element (Defn. 1).
Let \(A, B\) be two sets. Then there exists either an injection of \(A\) into \(B\) (\(o(A) \preceq o(B)\)) or an injection of \(B\) into \(A\) (\(o(B) \preceq o(A)\)) (at least one).
In other words, \(\preceq\) on cardinal numbers forms a chain.
Proof sketch:
- Let \(L := \{ (A_{i}, B_{i}, f_{i}) : A_{i} \subset A, B_{i} \subset B, f_{i}: A_{i} \to B_{j} \text{ is bijective} \}\). Define \((A_{i}, B_{j}, f_{i}) \preceq (A_{j}, B_{j}, f_{j})\) iff \(A_{i} \subset A_{j}\), \(B_{i} \subset B_{j}\), and \(f_{i} = f_{j} |_{A_{i}}\). Show that \(L\) is a poset.
Show that any chain in \(L\) has an upper bound. By Zorn’s Lemma, \(L\) contains a maximal element.
Proof: For any chain \(\{ (A_{i}, B_{i}, f_{i}) : i \in I \} \subset L\), we construct an upper bound in the followings: Let \(A_0 = \cup _{i \in I} A_{i}, B_{0} = \cup _{i\in I} B_{i}\). For every \(a \in A_0\), \(\exists A_{i}\) s.t. \(a \in A_{i}\). In this case, set \(f(a) = f_{i}(a)\). We can check that (1) \(f_0\) is well defined by the property of chain, (2) \(f_0\) is bijective, and (3) \((A_0, B_0, f_0)\) is indeed an upper bound.
Let \((A ^{*}, B ^{*}, f ^{*})\) be a maximal element. Show that either \(A ^{*} = A\) or \(B ^{*} = B\). Then, we have either an injection from \(A\) into \(B ^{*} \subset B\) or an injection from \(B\) into \(A ^{*} \subset A\), which concludes the proof.
Proof: Suppose not, then there exists \(a \in A \setminus A ^{*}, b \in B \setminus B ^{*}\). We can construct a bijection \(g: A ^{*} \cup \{ a \} \to B ^{*} \cup \{ b \}\) by \(g(x) = f ^{*}(x)\) for \(x \in A ^{*}\) and \(g(x) = b\) for \(x = a\). Then, \((A ^{*} \cup \{ a \}, B ^{*} \cup \{ b \}, g)\) dominates \((A ^{*}, B ^{*}, f ^{*})\).
2.3. Arithmetic of Cardinal Numbers
2.3.1. Addition
Let \(d, e\) be two cardinals. Define \(d + e = o(D \sqcup E)\) for some sets \(D, E\) satisfying \(o(D) = d, o(E) = e, D \cap E = \emptyset\).
P.S.: We can always find such disjoint sets \(D, E\). Let \(\hat{D}, \hat{E}\) be any two sets with the corresponding cardinals, then \((D \times \{ 0 \}) \cap (E \times \{ 1 \}) = \emptyset\).
Any infinite set \(A\) can be expressed as some disjoint union of countably infinite sets. The union itself is not necessarily countable.
We appeal to Zorn’s Lemma.
Let \(L = \{ C: C = \{ B_{i} \}_{i \in I}, B_{i} \subset A \text{ are countable infinite and pairwise disjoint } \}\). \(L\) consists of all possible collections of subsets of \(A\) required by the lemma. Define \(\preceq\) on \(L\) by \(C \preceq \hat{C}\) iff \(C \subset \hat{C}\). Consider an arbitrary chain \(\mathcal{C} = \{ C_{i} \}_{i \in I_0}\) in \((L, \preceq)\). Clearly, \(\mathcal{C}\) has an upper bound \(\overline{C} = \cup _{i \in I_0} C_{i}\). By Zorn’s Lemma, \((L, \preceq)\) has a maximal element, say \(C ^{*} = \{ B_{i} \}_{i \in I}\).
We want to construct a union required by the lemma using \(C ^{*}\). If \(A = \cup _{i \in I} B_{i}\), we are done. Suppose \(A \supsetneq \cup _{i \in I} B_{i}\). Let the remaining part be \(R = A \setminus \cup _{i \in I} B_{i}\). \(R\) is disjoint with any element in \(C ^{*}\).
- If \(R\) is countably infinite, then \(C ^{*} \cup \{ R \} \in L\) dominates \(C ^{*}\), which is a contradiction.
- If \(R\) is uncountable, we can take a countably infinite subset \(\hat{R} \subset R\). Similarly, this will lead to a contradiction.
- Thus, \(R\) has to be finite. We counstruct \(A = \{ C_{i_0} \cup \{ R \} \} \sqcup (\sqcup_{i \in I, i \neq i_0} C_{i})\).
Any infinite set \(A\) can be written as \(A = B \sqcup C\) where \(A, B, C\) all have the same cardinals.
By the last lemma, we can write \(A = \sqcup_{i} A_{i}\), where every \(A_{i}\) is countably infinite. Then, for each \(A_{i}\), we can always write \(A_{i} = B_{i} \sqcup C_{i}\), where \(B_{i}, C_{i}\) are countably infinite and have the same cardinal with \(A_{i}\). Then, set \(B = \sqcup_{i} B_{i}\), \(C = \sqcup_{i} C_{i}\).
Let \(d, e\) be cardinals s.t. \(d \leq e\) and \(e\) is infinite. Then, \(d + e = e\).
First note that \(e \preceq d + e\) (\(I: E \to E \cup D\) is an injection). The last lemma says \(e + e = e\). Thus, \(d \preceq e\) and \(e \preceq e\) imply \(d + e \preceq e\).
2.3.2. TODO Multiplication
Let \(d, e\) be two cardinals. Define \(d e = o(D \times E)\) for some sets \(D, E\) satisfying \(o(D) = d, o(E) = e\).
E.g., we’ve seen that \(\aleph_{0} \aleph_{0} = \aleph_{0}\).
Given an infinite cardinal \(d\), \(d d = d\).
Let \(D\) be a representative set of \(d\), i.e., \(o(D) = d\).
TODO
Let \(d, e\) be two cardinals. If \(d \preceq e\), \(d \neq 0\), and \(e\) is infinite, then \(de = e\).
Since \(d \neq 0\), it’s easy to see \(e \preceq de\). Since \(d \preceq e\), \(de \preceq ee\), which is equal to \(e\). By the anti-symmetry, \(e = de\).
2.3.3. TODO Exponentiation
Let cardinals \(d, e \neq 0\). Let sets \(D, E\) represent \(d, e\), resp. We denote \(\Hom(E: D)\) to be the set of all functions \(: E \to D\) (sometimes denoted as \(D ^{E}\)). Then, \(d ^{e}\) is defined to be the cardinal number of \(\Hom(E : D)\).
Let \(D\) be a set, \(d = o(D)\). We want to justify previous definition 1 of cardinals of power sets.
We denote \(o(\mathcal{P}(D)) = 2 ^{d}\). Since \(o(\Hom(D: \{ 0,1 \})) = 2 ^{d}\), we want to show that there is a bijection between \(\mathcal{P}(D)\) and \(\Hom(D: \{ 0,1 \})\). Consider the characteristic function \(\chi_{D_0} : D \to \{ 0,1 \}\), \(\chi_{D_0}(x) = 1\) if \(x \in D_0\) and 0 otherwise. Then the mapping \(D_0 \mapsto \chi_{D_0}\) for all \(D_0 \in \mathcal{P}(D)\) is a bijection.
\(2 ^{\aleph_{0}} = c\).
- \(2 ^{\aleph_{0}} \preceq c\): Consider the subset of \(\mathbb{R} \) \(\{ 0.a_1 a_2 \dots | a_{n} \in \{ 2, 3 \}, n \in \mathbb{N} \}\). We pick two digits other than 0 and 9 here to avoid decimal represenattions that correspond to the same real number. Then, there is clearly a bijection between \(\{ 2, 3 \} ^{\mathbb{N} }\) and the set. Thus, \(2 ^{\aleph_{0}} \preceq c\).
- \(c \preceq 2 ^{\aleph_{0}}\): Consider the representation of real numbers in the base 2. Every real number can be represent by \(b_{n} \dots b_2 b_1 . a_1 a_2 \dots \), where all digits are 0 or 1, and \(n\) is finite. Note that a representation ending in infinitely many 1’s is equal to (corresponding to the same real number) another one that ends in infinitely many 0’s. This means that there is an injective function \(: \mathbb{R} \to \) all the representations. Since the set of all possible representations is bijective to \(\{ 0,1 \} ^{\mathbb{N} }\), \(c \preceq 2 ^{\aleph_{0}}\).
By the anti-symmetry, \(2 ^{\aleph_{0}} = c\).
- If cardinals \(d_1, d_2 \succeq 2\) and \(e\) is infinite, then \((d_1 d_2) ^{e} = d_1 ^{e} d_2 ^{e}\).
- \(d ^{e_1 + e_2} = d ^{e_1} d ^{e_2}\).
- Let \(d, e, f\) be cardinals. Then \((d ^{e}) ^{f} = d ^{e ^{f}}\).
TODO
3. Well-Ordering
3.1. Well-Ordered Sets
A well-ordered set is a chain in which every non-empty subset has a least element (Defn. 1).
Properties:
- An infinite well-ordered set has an infinite ascending sequence: Repeatedly take the least element of the complement subset.
- Any subset of a well-ordered set is well-ordered with the relative ordering (restriction).
- In a well-ordered set, every subset with a upper bound has a supremum.
A chain is well-ordered iff it does not contain an infinite descending sequence.
Proof: easy.
A poset satisfies the descending chain condition if it contains NO infinite descending sequence.
An order ideal in a poset \((L, \preceq)\) is a subset \(I \subset L\) s.t. if \(x \in I\) and \(y \in L, y \preceq x\), then \(y \in L\).
Let \(a \in L\), where \(L\) is a poset. A segment \(S(a)\) determined by \(a\) is the set \(\{ x \in L: x \prec a \}\).
An ideal in a well-ordered set \(C\) is either all of \(C\) or a segment of \(C\).
Let \(I \subsetneq C\) be an ideal that is not all of \(C\). Let \(a\) be the least element of \(I ^{C}\).
We claim \(I = S(a)\). If \(x \prec a\), then \(x \in I\) for if \(x \in I ^{C}\) we could contradict minimality of \(a\). Thus, \(S(a) \subset I\). Conversely, if \(x \in I\) then \(x \prec a\) for if \(a \preceq x\) then this would imply \(a \in I\). Thus, \(I \subset S(a)\).
If every segment of a chain \(C\) is well-ordered, then \(C\) is well-ordered.
We prove the contrapositive. If \(C\) is not well-ordered, by definition, then it contains an infinite descending sequence \(a_1 \succ a_2 \succ a_3 \succ \dots \). Consider the segment \(S(a_1) = \{ x \in C: x \prec a_1 \}\). \(S(a_1)\) itself has no minimal element and thus is not well-ordered. Thus, the contrapositive is true.
We say two sets \(A\) and \(B\) are order-isomorphic if there is a bijection \(f: A \to B\) such that \(\forall a_1, a_2 \in A, f(a_1) \preceq f(a_2) \iff a_1 \preceq a_2\).
A well-ordered set cannot be order-isomorphic to any of its segments.
Suppose on the contrary that the well-ordered \(C\) is order-isomorphic to the segment \(S(a)\), \(a \in C\), via \(f: C \to S(a)\). Then, for any \(c \in C\), \(f(c) \in S(a)\), implying \(f(c) \prec a\). Specially, \(f(a) \prec a\). By the order-perserving property of \(f\), we have \(a \succ f(a) \succ f(f(a)) \succ \dots \). Thus, we find an infinite descending sequence in \(C\), which contradicts the well-ordering of \(C\).
Alternative: Let \(T := \{ x \in C: f(x) \prec x \} \neq \emptyset\). Since \(C\) is well-ordered, \(T \subset C\) must have a least element, say \(b\). As an element in \(T\), \(b\) satisfies \(f(b) \prec b\). Since \(f\) is order-preserving, this implies \(f(f(b)) \prec f(b)\). Thus, \(f(b) \in T\). However, \(b\) is the minimal element, so this is a contradiction.
Since we only utilize the property that any non-empty subset in \(C\) has a least element, the same proof with \(C\) replaced with a non-empty subset still applies.
Mathematical induction is equivalent to \(\mathbb{N} \) being well-ordered.
The principle of transfinite induction is its extension to general well-ordered sets.
Let \(C\) be well-ordered. If \(A \subset C\) satisfies that \(x \in A\) whenever \(S(x) \subset A\), then \(A = C\).
Prove the contrapositive: Suppose \(A \neq C\), let \(x \in C \setminus A\) be the least element. Then, by minimality of \(x\), \(S(x) = \{ y \in C : y \prec x \} \subset A\), but \(x \notin A\).
Let \(A\) and \(B\) be well-ordered sets. Then either \(A\) is order isomorphic to an ideal of \(B\) or \(B\) is order isomorphic to an ideal of \(A\).
P.S.: According to Defn. 1, this says that any two ordinals are comparable (in that specifically defined order). This theorem is parallel to Thm. 1.
TODO: Intuition?
Suppose on the contrary that both statements fail. Call an element \(a \in A\) good if \(\exists b \in B\) such that \(S(a) \cong S(b)\) via some order isomorphism. By Thm. 1, for a good element \(a\), the \(b\) is unique. Let \(I\) be the set of all good elements in \(A\). By the uniqueness of the corresponding \(b\), we can define a map \(f: I \to B\) by \(f(a) = b\).
Then, we check
\(I\) is an ideal in \(A\).
Suppose \(x \in I\), \(y \in A\), and \(y \preceq x\). Then, \(\exists b \in B\) such that \(S(x) \overset{\phi}{\cong} S(b)\) for some \(\phi\). Consider \(S(y) = \{ z \in A: z \prec y \} \subset S(x)\). For any \(a \in A\), \(a \in S(y) \iff a \prec y \iff \phi(a) \preceq \phi(y)\) by \(\phi\) being order-preserving. Note that \(\phi(S(x)) \subset S(b)\), so \(\phi(y) \prec b\) and \(S(\phi(y)) \prec S(b)\). It is easy to show that \(\phi|_{S(y)}: S(y) \to \phi(S(y))\) is an order-isomorphism. Then, \(y\) is a good element. Thus, \(I\) is an ideal.
- \(f\) is injective: Definition + Thm. 1.
\(f\) is order-preseving:
Assume \(a_1, a_2 \in I\), \(a_1 \preceq a_2\), \(b_1 = f(a_1)\), \(b_2 = f(a_2)\). First show that there exists an order-surjection \(: S(b_2) \to S(b_1)\) by showing an order-surjection \(: S(a_2) \to S(a_1)\). Then, disprove \(b_2 \prec b_1\), which leads to an order-isomorphism \(: S(b_1) \to S(b_1)\).
Let \(J\) be the image of \(f\), i.e., \(f(I)\), then \(J\) is an ideal in \(B\). Then, \(I \overset{f}{\cong} J\):
Let \(x \in J, y \in B, y \preceq x\). There exists a unique \(a \in I\) s.t. \(f(a) = x\), \(S(a) \cong_{\phi} S(x)\). Consider \(\phi ^{-1}(y)\).
By the assumption, \(I \neq A\) and \(J \neq B\). Let \(x\) be the least element in \(I ^{C}\) and \(J\) be the least element in \(J ^{C}\). Since \(x\) is the least element in \(I ^{C}\), we have \(S(x) \subset I\). On the other hand, for any \(\hat{x} \in I\), \(S(\hat{x}) \overset{\phi}{\cong} S(\hat{y})\) for some \(\hat{y}\). If \(x \prec \hat{x}\), we have \(x \in S(\hat{x})\) and \(S(x) \overset{\phi}{\cong} S(\phi(\hat{y}))\), which contradicts with \(x\) not being a good element. Thus, \(I \subset S(x)\) and \(I = S(x)\). Similarly, we have \(S(y) = J\).
We know that \(S(x) \overset{f}{\cong} S(y)\), so \(x\) is a good element, contradicting with \(x \notin I\).
3.2. Any Set can be Well-ordered
Any set \(A\) can be well-ordered (\(\exists \) some order \(\prec\) on \(A\) s.t. \((A, \prec)\) is well-ordered).
Since our previous results are built on ZL 1, the following proof is actually for ZL \(\implies\) WO.
Let \(L := \{ (A_{i}, \preceq_{i}) : A_{i} \subset A, A_{i} \neq \emptyset, (A_{i}, \preceq_{i}) \text{ is well-ordered} \}\). The subscript in \(\prec_{i}\) emphasizes that elements in \(L\) are not only distinguished by the sets but also by the orders.
E.g., all singletons, \((\{ a \}, )\) for \(a \in A\), are in \(L\) with no choice of ordering. All two-elements subsets of \(A\), say \(\{ a, b \}\), appear in \(L\) twice as \(B_1 = (\{ a, b \}, \prec_{1}), a \prec_{1} b\) and \(B_2 = (\{ a, b \}, \prec_{2}), b \prec_{2} a\), and so on. A finite subsets of \(A\) with \(n\) elements appear precisely \(n!\) times in \(L\).
We define \(\preceq\) on \(L\) as \((A_{i}, \preceq_{i}) \preceq (A_{j}, \preceq_{j})\) iff (1) \(\prec_{i}\) is the restriction of \(\preceq_{j}\) to \(A_{i}\) and (2) \(A_{i}\) is an ideal in \((A_{j}, \preceq_{j})\) and .
We claim that every chain in \(L\) possesses an upper bound. Let \((\{ (B_{i}, \preceq_{i}) \}, \preceq)\) be a chain in \(L\). We may natural exmaine whether \(B = \cup _{i} B_{i}\) equipped with some order can be the upper bound of the chain in \(L\). We have to
Define an order \(\hat{\preceq}\) on \(B\) s.t. \(\preceq_{i}\)’s are restrictions of \(\hat{\preceq}\).
Let \(x, y \in B, x \neq y\). It is easy to see that \(x, y \in B_{i}\) for some \(i\). Since \(B_{i}\) itself is a chain (well-ordered), exactly one of \(x \prec_{i} y\) and \(y \prec_{i} x\) holds. We set \(\hat{\prec}\) to be \(\prec_{i}\) on the comparison of \(x\) and \(y\). This is well-defined because \(\{ (B_{i}, \preceq_{i}) \}\) is a chain.
Show that \(B_{i}\) is an ideal in \((B, \hat{\preceq})\):
Let \(x \in B_{i}, y \in B, y \hat{\preceq} x\). \(y \in B_{j}\) for some \(j\). If \(j \leq i\), then \(y \in B_{j} \subset B_{i}\). If \(j > i\), by definition of \(\preceq\), \(B_{i}\) is an ideal in \((B_{j}, \preceq_{j})\). Then, \(y \in B_{j}, y \preceq_{j} x \implies y \in B_{i}\). Thus, \(B_{i}\) is an ideal in \((B, \hat{\preceq})\).
Show that \((B, \hat{\preceq}) \in L\), i.e., it is a well-ordered set.
By Thm. 1, it suffices to show that
It is a chain.
First we prove that it is a poset. (1) Reflexivity is trivial. (2) Transitivity: If \(x \hat{\preceq} y\) and \(y \hat{\preceq} z\), then this will present in a single \((B_{i}, \preceq_{i})\). By the transitivity of \(\preceq_{i}\) there, \(x \preceq_{i} z\), and hence \(x \preceq z\). (3) Anti-symmetry: Similar.
Similarly, for any \(x, y \in B\), they will present in a single \(B_{i}\), and since \(B_{i}\) is a chain, they are comparable by \(\preceq_{i}\) and hence by \(\preceq\).
- Every segment \(S(x), x \in B\) is well-ordered. TODO
Any set of cardinals is well-ordered in the natural ordering we introduced on cardinal numbers.
Suppose the opposite. Then by Thm. 1, there exist an infinite descending sequence \(d_1 \succ d_2 \succ \dots \). Let \(D_{i}\) be a set with \(o(D_{i}) = d_{i}\). By Axiom. 1, \(D_{i}\) equipped with some order is well-ordered. Applying Thm. 1 to \(D_{i}\) and \(D_1\), in view of \(d_1 \succ d_{i}\), it must be the case that \(D_{i}\) is order-isomorphic to a segment (since not the entire \(D_1\)) in \(D_1\), say \(S(b_{i})\). Then, we have \(o(S(b_{i})) = d_{i} \succ d_{i+1} = o(S(b_{i+1}))\). If \(b_{i} \preceq b_{i+1}\), then \(S(b_{i}) \subset S(b_{i+1})\) and \(o(S(b_{i})) \preceq o(S(b_{i+1}))\), which is a contradiction (with the natural ordering of cardinals). Thus, \(b_{i} \succ b_{i+1}\) (by the order on \(D_{i}\)) and we find an infinite descending sequence in \(D_1\) which violates the well-ordering of \(D_{1}\).
3.3. Ordinal Numbers
We attach to every well-orderd set an ordinal number. Two well-ordered sets have the same ordinal number iff they are order-isomorphic. We define ordering on ordinal numbers as follows: Let \(\alpha, \beta\) be ordinal numbers and let \(A, B\) be well-ordered sets with corresponding ordinals, then we define \(\alpha \preceq B\) iff \(A\) is order-isomorphic to an ideal of \(B\).
This definition is easily seen to be well-defined.
The set of all ordinal numbers is a chain.
Reflexivity is obvious.
Transitivity: Let well-ordered sets \(A, B, C\) have the ordinal \(\alpha, \beta, \gamma\), resp. Assume \(\alpha \preceq \beta\) and \(\beta \preceq \gamma\). Then, \(A\) is order-iso. to \(I_{B}\) via some \(\phi\) and \(B\) is order-iso. to \(I_{C}\) via some \(\psi\). Clearly, \(\psi|_{I_{B}} \circ \phi\) is an order-iso. from \(A\) to \(\psi(I_{B})\). We want to show that \(\psi(I_{B})\) is an ideal in \(C\).
Let \(x \in \psi(I_{B}) \subset I_{C}\), then there is a unique \(b_{x} \in I_{B}\) with \(\psi(b_{x}) = x\). For any \(y \in C\) with \(y \preceq x\), we have \(y \in I_{C}\) (ideal). Thus, there is a unique \(b_{y} \in B\) with \(\psi(b_{y}) = y\). Additionally, \(b_{y} \preceq b_{x}\) (order-preserving), so \(b_{y} \in I_{B}\) (ideal), and hence \(y \in \psi(I_{B})\).
- Antisymmetry: If \(\alpha \leq \beta\) and \(\beta \leq \alpha\), by transitivity, then \(\alpha \leq \alpha\). This means that \(A\) is order-isomorphic to one of its ideal. From Thm. 1, we know that the only possibility is \(\alpha = \alpha\).
Let \(\alpha\) be any ordinal. Then the set \(\{ \beta: \beta < \alpha \}\) is a well-ordered set with ordinal number \(\alpha\).
Let \(A\) be a well-ordered set with ordinal-number \(\alpha\). Show that the map \(\beta \to b\), where \(b\) satisfies that \(S(b)\) has ordinal number \(\beta\), is an order-isomorphism \(\{ \beta: \beta < \alpha \} \to A\).
By Axiom. 1, any set of ordinal numbers is well-ordeded.
3.4. TODO Listing Ordinal Numbers
- From ordinals to cardinals
We define a map from ordinals to cardinals: For any ordinal \(\alpha\), let \(A\) be a well-ordered set with ordinal \(\alpha\), then \(\alpha \mapsto o(A)\).
This mapping is:
- Well-defined: If two well-ordered sets are order-isomorphic (same ordinal), then necessarily they are isomorphic (same cardinal).
- Surjective: Thm. 1, any set can be well-ordered.
- Not injective: See below the notion of countable ordinals.
Let \(d\) be any cardinal. The unique smallest ordinal mapped to \(d\), i.e. the least element among all ordinals mapped to \(d\), is called the initial ordinal of \(d\).
Consider the set of finite ordinals (ordinals of finite sets)
\begin{equation} \label{eq:set-fin-ord} \{ 0, 1, 2, \dots , n, \dots \}. \tag{I} \end{equation}Clearly, each of them maps to the same finite cardinal (and we use the same notation). Let \(\omega\) be the ordinal of the set \eqref{eq:set-fin-ord}. Then, by Thm. 1, the set \eqref{eq:set-fin-ord} is just \(\{ \beta: \beta < \omega \}\), meaning that \(\omega\) is the first infinite ordinal. Meanwhile, \(\omega\) is the initial ordinal of \(\aleph_{0}\).
Consider the set
\begin{equation} \label{eq:set-fin-ord-omega} \{ 0, 1, 2, \dots , n, \dots , \omega \}. \tag{II} \end{equation}Denote by \(\omega + 1\) the ordinal of the set \eqref{eq:set-fin-ord-omega}. Note that we can construct an isomorphism from \eqref{eq:set-fin-ord-omega} to \eqref{eq:set-fin-ord} (\(\omega \mapsto 0\) and \(n \mapsto n + 1\) otherwise), but not an order isomorphism (\eqref{eq:set-fin-ord} is a segment of \eqref{eq:set-fin-ord-omega}). Thus, \(\omega + 1 \mapsto \aleph_{0}\) but \(\omega + 1 \neq \omega\).
Let \(\alpha\) be an ordinal \(\alpha\) and \(A\) be a set with ordinal \(\alpha\). We say \(\alpha\) is countable if \(o(A) = \aleph_{0}\) (isomorphic to a countable set).
To reiterate, \(\omega\) is the least element among all the countable ordinals and hence the initial ordinal of \(\aleph_{0}\).
Repeating the above process, we have
\begin{equation} \label{eq:set-fin-ord-omega-fin} \{ 0, 1, \dots , n, \dots , \omega, \omega + 1, \dots , \omega + n, \dots \}. \tag{III} \end{equation}Note that \(\{ \omega + n: n \in \mathbb{N} \}\) are still countable ordinals (by constructing the similar shifted mappings). Denote by \(2 \omega\) the ordinal of the set \eqref{eq:set-fin-ord-omega-fin}.
An ordinal \(\alpha\) is a limit ordinal if it has no immediate predecessor (\(\alpha - 1\) does not exist).
\(\omega\) is the first limit ordinal, and \(2 \omega\) is the second limit ordinal. By repeating this we have limit ordinals \(3 \omega, 4 \omega, \dots \). Note that \(\{n \omega: n \in \mathbb{N} , n \geq 2\}\) are still countable ordinals (their corresponding sets can be viewed as “\(n\) copies” of \(\mathbb{N} \), which are isomorphic to \(\mathbb{N} \)).
The \(\omega\)-th limit ordinal is denoted by \(\omega ^2\), and the \(2\omega\)-th \(\omega ^3\), and the \(n \omega\)-th \(\omega ^{n+1}\) for \(n \in \mathbb{N} \). Fact (TODO): They are still coutable ordinals.
And we have \(\omega ^{\omega^{\omega}}, \omega ^{\omega ^{\omega ^{\omega}}}, \dots \). (TODO) They are still countable ordinals.
- Aleph Numbers
- \(\aleph_{1}\) is defined to be the cardinal of the set of all countable ordinals. Let \(\Omega\) be the initial ordinal of \(\aleph_{1}\). \(\Omega\) is the first uncountable ordinal (TODO)
3.5. The Axiom of Choice
Let \(A\) be any set. Then there exists a function \(f\) defined on nonempty subsets of \(A\) which assigns to every such subset (input) one of its member (output): \(f: A_{i} \mapsto a\) for some \(a \in A_{i}\).
AC \(\implies\) ZL \(\implies\) WO \(\implies\) AC.
Let \(L\) be a partially ordered set in which every chain has a least upper bound. Then there CANNOT exist a function \(g: L \to L\) such that for every \(x\) in \(L\), \(g(x)\) is directly above \(x\) (i.e., \(g(x) > x\) and no element of \(L\) lies strictly between \(g(x)\) and \(x\)).
Let \(L\) be a partially ordered set in which every chain has a least upper bound. Then there CANNOT exist a function \(g: L \to L\) such that for every \(x\) in \(L\), \(g(x) > x\).
3.6. TODO The Continuum Problem
Conjecture, Continuum hypothesis: \(\aleph_{1} = c\).
Conjecture, Generalized continuum hypothesis: \(2 ^{\aleph_{\lambda}} = \aleph_{\lambda + 1}\) for every ordinal \(\lambda\).