Linear-Time Temporal Logic (LTL)

\( \renewcommand{\vec}[1]{\mathbf{#1}} \newcommand{\mat}[1]{\mathbf{#1}} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\pto}{\rightharpoonup} \DeclareMathOperator{\LIM}{LIM} \DeclareMathOperator{\nimplies}{\centernot\implies} \newcommand{\neimplies}{\rotatebox[origin=c]{30}{\(\implies\)}} \newcommand{\seimplies}{\rotatebox[origin=c]{-30}{\(\implies\)}} % set and topology \newcommand{\cl}[1]{\overline{#1}} \DeclareMathOperator{\diam}{diam} % algebra \DeclareMathOperator{\Hom}{Hom} \DeclareMathOperator{\Span}{Span} \DeclareMathOperator{\Ran}{Ran} \DeclareMathOperator{\Ker}{Ker} \DeclareMathOperator{\Nul}{Nul} \DeclareMathOperator{\Col}{Col} \DeclareMathOperator{\Row}{Row} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\rank}{rank} \DeclareMathOperator{\proj}{proj} \DeclareMathOperator{\diag}{diag} % probability and statistics \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\prob}{\mathbb{P}} \DeclareMathOperator{\indep}{\perp \!\!\! \perp} \DeclareMathOperator{\Var}{\mathbb{V}} \DeclareMathOperator{\Cov}{Cov} \DeclareMathOperator{\Cor}{Cor} % programs \newcommand{\sem}[1]{[\![ #1 ]\!]} \newcommand{\ans}[1]{[\![ #1 ]\!]} \DeclareMathOperator{\Val}{Val} \DeclareMathOperator{\Vars}{Vars} \DeclareMathOperator{\AExp}{AExp} \DeclareMathOperator{\BExp}{BExp} \DeclareMathOperator{\mAND}{\mathsf{and}} \DeclareMathOperator{\mOR}{\mathsf{or}} \DeclareMathOperator{\mNOT}{\mathsf{not}} \DeclareMathOperator{\mTRUE}{\mathsf{true}} \DeclareMathOperator{\mFALSE}{\mathsf{false}} \DeclareMathOperator{\mSKIP}{\mathsf{skip}} \DeclareMathOperator{\mWHILE}{\mathsf{while}} \DeclareMathOperator{\mDO}{\mathsf{do}} \DeclareMathOperator{\mOD}{\mathsf{od}} \DeclareMathOperator{\mIF}{\mathsf{if}} \DeclareMathOperator{\mFI}{\mathsf{fi}} \DeclareMathOperator{\mTHEN}{\mathsf{then}} \DeclareMathOperator{\mELSE}{\mathsf{else}} \DeclareMathOperator{\mFOR}{\mathsf{for}} \DeclareMathOperator{\mTERM}{\mathsf{Term}} \DeclareMathOperator{\mHALT}{\mathsf{Halt}} \DeclareMathOperator{\mBREAK}{\mathsf{Break}} \DeclareMathOperator{\mCONTINUE}{\mathsf{Continue}} \DeclareMathOperator{\mCOND}{\mathsf{cond}} \DeclareMathOperator{\mUNDEFINED}{\mathsf{undefined}} \)

1. Intro

Relation between the game view and automaton view:

\(O_1, Outcome(v, \sigma_{1}, \sigma_{2})\) etc. can be seen as sets of words, i.e., languages. Checking \(Outcome(v, \sigma_{1}, \dots ) \subseteq O_1\) is actually checking if the first language is the subset of the second one.

2. Traces

Let \(P\) be a finite set of atomic propositions and \(\Sigma = 2 ^{P}\). A trace is an infinite word over \(\Sigma\), i.e., any element \(\tau \in \Sigma ^{\omega}\).

E.g., consider a traffic light, in which \(P = \{ r, g, y \}\) and \(\Sigma\) has 8 states. We only accepts state in which exactly one of the three colors is on, so an accepting trace is like \(r, g, y, r, g, y, \dots \). We can easily construct Buchi automata that accepts (exactly) this kind of traces.

3. LTL Syntax and Informal Semantics

The syntax of LTL formulas is defined by \[ \phi := \mTRUE | p | \phi_{1} \lor \phi_{2} | \neg \phi | \bigcirc \phi | \phi_{1} U \phi_{2} \] (\(\mFALSE, \land, \implies \) can be written using those expressions, e.g., \(\phi_{1} \implies \phi_{2} := \neg \phi_{1} \lor \phi_{2}\)), where

\(p \in P\): \(p\) holds at the current time.
\(\bigcirc \phi\) (next): \(\phi\) holds at the next point of time. Sometimes written as \(X \phi\).
\(\phi_{1} U \phi_{2}\) (until): \(\phi_{1}\) holds until at some point in the future \(\phi_{2}\) holds.

Other formulas can be written using formal formulas:

\(\lozenge \phi\) (eventually): There is some point in the future when \(\phi\) holds. Also written as \(F \phi\). \(\lozenge \phi = \mTRUE U \phi\) (true, which always holds, until \(\phi\) holds).
\(\square \phi\) (globally): At every point of time, \(\phi\) holds. Also written as \(G \phi\). \(\square \phi = \neg \lozenge \neg \phi\).

E.g., \(\square \lozenge g\) means that \(g\) is on infinitely often (Buchi) and \(\lozenge \square g\) means that \(g\) is always on after finitely many steps (coBuchi)

4. Formal Semantics

Let \(\phi\) be an LTL formula. The semantics \(\sem{\phi} \subseteq \Sigma ^{\omega}\) is the set of all traces that satisfy \(\phi\).

Let \(\tau = \tau_{0} \tau_{1} \dots \), where \(\tau_{i} \in \Sigma\). \(\tau[i .. j] = \tau_{i} \dots \tau_{j}\), \(\tau[i..) = \tau_{i} \tau_{i+1} \dots \). We write \(\tau \vDash \phi\) if \(\tau\) satisfies \(\delta\). Semantics of specific formulas are given below:

\[ \infer{\tau \vDash \mTRUE}{} \]
\[ \infer{\tau \vDash \neg \phi}{\tau \centernot\vDash \phi} \]
\[ \infer{\tau \vDash p}{p \in \tau_{0}} \]
\[ \infer{\tau \vDash \phi_{1} \lor \phi_{2}}{\tau \vDash \phi_{1}}, \infer{\tau \vDash \phi_{1} \lor \phi_{2}}{\tau \vDash \phi_{2}} \]
if \(\phi\) holds for the suffix starting from the next character, then it holds in the next point of time. \[ \infer{\tau \vDash \bigcirc \phi}{\tau[1 ..) \vDash \phi} \] Why cannot use \(\tau[i] \vDash \phi\)? Because \(\phi\) may involve the suffix property of words.
If \(\phi\) holds for some suffix, then it holds eventually. \[ \infer{\tau \vDash \lozenge \phi}{\exists i, \tau[i..) \vDash \phi} \]
\[ \infer{\tau \vDash \square \phi}{\forall i, \tau[i..) \vDash \phi} \]
\[ \infer{\tau \vDash \phi_{1} U \phi_{2}}{\exists j, (\tau[j ..) \vDash \phi_{2}) \land (\forall 0 \leq i < j, \tau[i ..) \vDash \phi_{1})} \]

5. Classical Objectives in LTL

For a \(p \in P\), we define \(A_{p} = \{ \sigma \in \Sigma | p \in \sigma \}\).

\(Reach(A_{p}) = \sem{\lozenge p}\).
\(Safe(A_{p}) = \sem{\square p}\).
\(Buchi(A_{p}) = \sem{\square \lozenge p}\).
\(coBuchi(A_{p}) = \sem{\lozenge \square p}\).

Let \(P = \{ 0, 1, \dots , d \}\) be the set of possible priorities under a priority function \(q\).

\(Parity(q) = \sem{\square \lozenge 0 \lor (\neg \square \lozenge 0 \land \neg \square \lozenge 1 \land \square \lozenge 2) \lor (\neg \square \lozenge 0 \land \neg \square \lozenge 1 \land \neg \square \lozenge 2 \land \neg \square \lozenge 3 \land \square \lozenge 4) \dots }\)

6. Equivalence of LTL Formulas

\(\phi_{1}\) and \(\phi_{2}\) are semantically equivalent, and denoted by \(\phi_{1} \equiv \phi_{2}\), if \(\sem{\phi_{1}} = \sem{\phi_{2}}\).

E.g., \(\square (\phi_{1} \lor \phi_{2})\) is not equivalent to \(\square \phi_{1} \lor \square \phi_{2}\), because we may have words whose suffices satisfy \(\phi_{1} \land \neg \phi_{2}\) and \(\neg \phi_{1} \land \phi_{2}\) alternately, but not \(\phi_{1} \land \phi_{2}\) globally.

\(\phi_{1} U \phi_{2} \equiv \phi_{2} \lor (\phi_{1} \land \bigcirc (\phi_{1} U \phi_{2}))\) (analogous to while). \(\lozenge \phi \equiv \phi \lor \bigcirc \lozenge \phi\). \(\square \phi \equiv \phi \lor \bigcirc \square \phi\).

7. Denotational Semantics

\(\sem{\mTRUE} := \Sigma ^{\omega}\)
\(\sem{p} := \{ \tau \in \Sigma ^{\omega} | p \in \tau_{0} \}\)
\(\sem{\phi_{1} \lor \phi_{2}} := \sem{\phi_{1}} \cup \sem{\phi_{2}}\), \(\sem{\phi_{1} \land \phi_{2}} := \sem{\phi_{1}} \land \sem{\phi_{2}}\).
\(\sem{\neg \phi} := \Sigma ^{\omega} \setminus \sem{\phi}\)
\(\sem{\bigcirc \phi} := \{ \tau \in \Sigma ^{\omega} | \tau[1 ..) \in \sem{\phi} \} = \Sigma \sem{\phi}\)

To define \(\sem{\phi_{1} U \phi_{2}}\): Define \(f_{\phi_{1}, \phi_{2}}(X) := \sem{\phi_{2}} \cup (\sem{\phi_{1}} \cap \Sigma X)\) (abbreviated to \(f\) below), which is from the equivalence of \(\phi_{1} U \phi_{2}\). \(f: 2 ^{\Sigma ^{\omega}} \to 2 ^{\Sigma ^{\omega}}\). We expect to have \(f(\sem{\phi_{1} U \phi_{2}}) = \sem{\phi_{1} U \phi_{2}}\). So \(\sem{\phi_{1} U \phi_{2}}\) is a fixed-point of \(f\).

The analysis of fixpoint of \(f\) is exactly the same as in the case of while. As a conclusion, \(\sem{\phi_{1} U \phi_{2}} = \) the least defined fixpoint of \(f\).

8. Generalized Non-deterministic Buchi Automata (GNBWs)

A Generalized Buchi Automaton is a Buchi Automaton with acceptance condition defined using multiple sets \(T_1, \dots , T_{k} \subseteq Q\). A run \(\varrho\) of the automaton is accepting if it visits each \(T_{i}\) infinitely many times.

Let \(A = (\Sigma, Q, Q_0, \phi, T_1, \dots , T_{k})\) be any arbitray GNBW. There is an NBW \(B\) such that \(L(B) = L(A)\).

On the other hand, an NBW is a GNBW with \(k = 1\). Together, they show that GNBW is eqully expressive as NBW.

Let \(B = (\Sigma, Q \times \{ 1, \dots , k \}, Q_0 \times \{ 1 \}, \delta', T_1 \times \{ 1 \} \cup \dots \cup T_{k} \times \{ k \})\), where

\begin{align*} \delta' (q, i, \sigma) = \begin{cases} (\delta(q, \sigma), i), & \text{if } q \notin T_{i}\\ (\delta(q, \sigma), i+1), & \text{if } q \in T_{i}, i \neq k\\ (\delta(q, \delta), 1), & \text{if } q \in T_{i}, i = k \end{cases}. \end{align*}

\(L(B) \subseteq L(A)\): An accepting word of \(B\) visits \(T_1 \times \{ 1 \} \cup \dots \cup T_{k} \times \{ k \}\) (finite set) infinitely often, then it must visit \(T_{j} \times \{ j \}\) infinitely often for some \(j\). Since between any two adjacent visits to \(T_{j} \times \{ j \}\) the word pass through all other \(T_{i} \times \{ i \}\), the word must visit all \(T_{i} \times \{ i \}\) infinitely often. Thus, the word is also accepted by \(A\).

\(L(A) \subseteq L(B)\): For any accepting word of \(A\), we can easily find a sequence of indices \(i_{1,1}, \dots , i_{1, k}, i_{2, 1}, \dots , i_{2, k}, i_{3, 1}, \dots \) such that \(i_{t, j} \in T_{j}\). Hence, we can map this word to an accepting word of \(B\).

9. From LTL formulas to NBWs

Model Checking: Given a formula and a program, check if the every run of the program satisfies the formula or not.

Intuitively, we will translate both the formula and the program to (nondeterministic Buchi) automata, and see if the language of the program is a subset of the language of the formula.

Basic Translations using structural induction:

\(\phi = \mTRUE\).
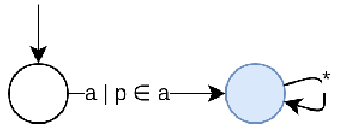
\(\phi = p\) (\(p \in P, a \in 2 ^{P}\))
\(\phi = \phi_{1} \lor \phi_{2}\). Union of NBWs.
\(\phi = \neg \phi '\). Complement NBW.
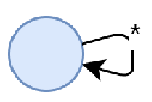
\(\phi = \bigcirc \phi'\). Let \(A_{\phi'}\) be the NBW for \(\phi'\). Then the NBW for \(\phi\) is an initial state with a \(*\) transition to each of the intial states of \(A_{\phi'}\) (ignore the first character).

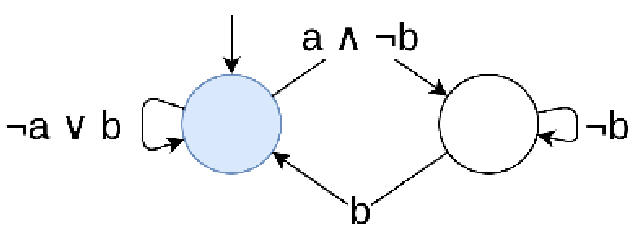
E.g., \(\sem{\square (a \to \lozenge b)}\)

10. From LTL formulas to GNBWs

\(\phi_{1} U \phi_{2}\). Note that \(\phi_{1}\) and \(\phi_{2}\) themselves can talk about properties about the future.

Let \(sf(\phi)\) be the set of subformulas of \(\phi\), defined by:

\(sf(\mTRUE) = \{ \mTRUE \}\)
\(sf(p) = p\)
\(sf(\phi_{1} \land \phi_{2}) = \{ \phi_{1} \land \phi_{2} \} \cup sf(\phi_{1}) \cup sf(\phi_{2})\)
\(sf(\neg \phi) = \{ \neg \phi \} \cup sf(\phi)\)
\(sf(\bigcirc \phi) = \{ \bigcirc \phi \} \cup sf(\phi)\)
\(sf(\phi_{1} \cup \phi_{2}) = \{ \phi_{1} \cup \phi_{2} \} \cup sf(\phi_{1}) \cup sf(\phi_{2})\)

Closure: we define the closure of \(\phi\) as \(cl(\phi) = \{ \psi, \neg \psi | \psi \in sf(\phi)\}\).

Intuitively, we want each state in the GNBW for \(\phi\) to be a set of subformulas and: For any accepting word \(w = w_0 w_1 \dots \), we have a run \(\rho = q_0 q_1 \dots \) over \(w\) such that each suffix \(w[i ..) \vDash \psi \forall \psi \in q_{i}\).

A subset \(q \subseteq cl(\phi)\) is elementary if:

It is a maximal consistent subset according to propositional logic, i.e.,
- for every \(\psi \in cl(\phi)\), \(\psi \in q \iff \neg \psi \notin q\)
- for every \(\psi_{1} \land \psi_{2} \in cl(\phi)\), \(\psi_{1} \land \psi_{2} \in q \iff \psi_{1} \in q \land \psi_{2} \in q\).
- if \(\mTRUE \in cl(\phi)\), then \(\mTRUE \in q\)
\(q\) respects the semantics of \(U\), i.e., for every \(\psi_{1} U \psi_{2} \in cl(\phi)\), we have:
- if \(\psi_{1} U \psi_{2} \in q\) and \(\psi_{2} \notin q\), then \(\psi_{1} \in q\).
- if \(\psi_{2} \in q\), then \(\psi_{1} U \psi_{2} \in q\).

For any LTL formula \(\phi\), there is a GNBW \(A\) such that \(L(A) = \sem{\phi}\).

Let GNBW \(A = (\Sigma, Q, Q_0, \delta, Acc)\), where \(Q\) consists of all the elementary subsets of \(cl(\phi)\), \(Q_0 = \{ q \in Q | \phi \in q \}\).

We want to encode the constraint (acceptance condition) into transitions. \(\delta(q, w_{i})\), \(w_{i} \in \Sigma\) is defined below:

If \(w_{i} \neq q \cap P\), then \(\delta(q, w_{i}) = \emptyset\). Because all atomic propositions in \(q\) should be satisfied by the first character of the suffix from this state
If \(w_{i} = q \cap P\), then \(\delta(q, w_{i})\) is the set of all \(q' \in Q\) that satisfy the following:
- For every \(\bigcirc \psi \in cl(\psi)\), \(\bigcirc \psi \in q \iff \psi \in q'\).
- For every \(\psi_{1} U \psi_{2} \in cl(\phi)\) , \(\psi_{1} U \psi_{2} \in q\) iff \(\psi_{2} \in q \lor (\psi_{1} \in q \land \psi_{1} U \psi_{2} \in q')\).

The target sets are defined below:

We set \(T_1 = Q\) and \(Acc\) to be the generalized Buchi condition. If \(\phi\) has no \(U\), then that is the only target set.
If \(\phi\) has \(U\), also define one target set \(T(\psi_{1} U \psi_{2})\) for each \(\psi_{1} U \psi_{2} \in cl(\phi)\): \(T(\psi_{1} U \psi_{2}) = \{ q \in Q | \psi_{1} U \psi_{2} \notin q \lor \psi_{2} \in q \}\). Visiting this set infinitely many times guarantees that once \(\psi_{1} U \psi_{2}\) is required in some state \(\psi_{2}\) will eventually be satisfied.
The target sets are \(T_1\) and \(T(\psi_{1} U \psi_{2})\)’s (if any).

\(|A|\) is exponential in \(|\phi|\) (think about closure).

For every LTL formula \(\phi\), there is an NBW \(B\) such that \(L(B) = \sem{\phi}\).

Since the convertion from the GNBW \(A\) to the NBW \(B\) can be done in polynomial time, \(|B|\) is also exponential in \(|\phi|\).