Automata
Prerequisite: ../game/game.html
1. Automata on Finite Words
A Deterministic Finite Automaton (DFA) is a tuple \(A = (\Sigma, Q, q_{0}, \delta, T)\) in which:
- \(\Sigma\) is a finite alphabet of letters.
- \(Q\) is a finite set of states.
- \(q_0 \in Q\) is the initial state.
- \(\delta: Q \times \Sigma \rightarrow Q\) is the transition function.
- \(T \subseteq Q\) is the set of accepting states.
A DFA operates on fintie words as follows: It starts from the initial state. Each each symbol from the alphabet is read sequentially. If the current state and symbol are \(q\) and \(a\) respectively, it transits to \(\delta(q, a)\).
A word is accepted if the (unique) run with that word ends in an accepting state. (P.S. if the transition corresponding to the input symbol is not available at the current state, then it directly leads to a rejection.)
The language of the automaton is the set of accepted words.
P.S., we denote the set of all finite words consisting of letters in \(\Sigma\) by \(\Sigma ^{*}\).
A Nondeterministic Finite Automaton NFA is a tuple \(A = (\Sigma, Q, Q_0, \delta, T)\) in which:
- \(\Sigma\) is a finite alphabet of letters
- \(Q\) is a finite set of states
- \(Q_0 \subseteq Q\) is the set of initial states
- \(\delta: Q \times \Sigma \to 2^Q\) is the transition function (changed, can transit to multiple states)
- \(T \subseteq Q\) is the set of accepting states
A word is accepted if there exists a run over the word ending in an accepting state.
1.1. Basic Closure Properties
Any NFA has a NFA complement.
2. Automata on Infinite Words (\(\omega\)-automata)
We denote the set of all infinite words consisting of letters in \(\Sigma\) by \(\Sigma ^{\omega}\).
A Deterministic Automaton on Infinite words is a tuple \(A = (\Sigma, Q, q_0, \delta, T, Acc)\) in which:
- \(\Sigma\) is a finite alphabet of letters.
- \(Q\) is a finite set of states
- \(q_0 \in Q\) is the initial state
- \(\delta: Q \times \Sigma \to Q\) is the transition function
- \(Acc\) is an acceptance condition formalizing when a run is acepting.
A Nondeterministic Automaton on Infinite words is a tuple \(A = (\Sigma, Q, Q_0, \delta, T)\) in which:
- \(\Sigma\) is a finite alphabet of letters.
- \(Q\) is a finite set of states
- \(Q_0 \subseteq Q\) is the initial state
- \(\delta: Q \times \Sigma \to 2 ^{Q}\) is the transition function
- \(Acc\) is an acceptance condition formalizing when a run is acepting.
The Automata on Infinite words with the acceptance condition being Buchi or Parity are called Buchi Automata and Parity Automata, resp.
2.1. Buchi Automata
A Buchi Automaton is an Automaton on Infinite words with Buchi acceptance condition: Let \(T \subseteq Q\) be the target set, a run \(\varrho\) is accepting if it visits T infinitely many times, i.e. \(\inf(\varrho) \cap T \neq \emptyset\).
We abbreviate Deterministics Buchi Automaton to DBW, and the nondeterministic one to NBW.
We call a language \(\omega\)-regular if it is the language of some NBW.
NBW are strictly more expressive than DBW:
- There is a language such that it is the language of some NBW, but is not language of any DBW.
- For any language, if it is the language of some DBW, then it must be the language of some NBW.
The second statement is trivial: we can make a DBW NBW by turning the initial state and the outputs of the transition function into sets of single element.
The first statement is proved by contradiction: Consider this NBW which accepts all words with finitely many zeros (grey nodes are target states):
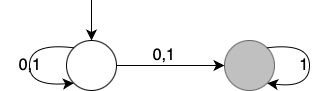
Suppose \(A\) is a DBW with the same language. Let \(n\) be the number of states in \(A\) (finite). Consider the following accepting infinite words:
- 11…1…, all ones: Let the first accepting state in the run be \(q_{i_1}\).
- 11…101…, same as the previous one except that a 0 is inserted right after \(q_{i_1}\): Let the first accepting state after the 0 be \(q_{i_2}\).
- and so on, the word with \(n\) 0s and the \(i\)-th 0 inserted right after \(q_{i+1}\): Let the first accepting state after the \(n\)-th 0 be \(q_{i_{n+1}}\).
By Pigeon principle, two among these accepting states, say \(q_{i_{j}}\) and \(q_{i_{k}}\), must be the same. Let the prefix of the last word before \(q_{i_{j}}\) be \(p\), and the subsequence between \(q_{i_{j}}\) and \(q_{i_{k}}\) (excluded) be \(r\). Starting from \(q_{i_{j}}\), the run of \(A\) returns to this state by reading \(r\). Then \(p (r ^{\omega}) \), the concatenation of \(p\) and infinite repetitions of \(r\), is also accepted, because it visits accepting states infinitely many times.
However, \(p (r ^{\omega})\) contains infinitely many zeros. This contradicts with the assumption. Thus, DBW with the same language does not exist.
2.1.1. Complementation of DBW
In the followings, we will call languages that can be recognized by some DBW “DBW languages”.
DBW languages are not closed under complementation. There is some DBW, such that we cannot find another DBW whose language is the complement of the language of the first DBW.
Consider the example in the last proof: We showed that there is no DBW of the language consisting of words with finitely many zeros. However, there exists a DBW of the language consisting of all words with infinitely many zeros:

2.1.2. Union of DBWs
DBW languages are closed under union. For any two DBWs, there is another DBW that recognize the union of languages of the two DBWs.
Let \(L_1, L_2\) be any two languages. Suppose \(L_1 = L(A_1), L_2 = L(A_2)\), where \(A_1 = (\Sigma, Q_1, q_{01}, \delta_{1}, T_1)\) and \(A_2 = (\Sigma, Q_2, q_{02}, \delta_{2}, T_2)\).
Consider the automaton that simulates the transitions of \(A_1, A_2\) at the same time: \(A = (\Sigma, Q_1 \times Q_2, (q_{01}, q_{02}), \delta, (T_1 \times Q_2) \cup (Q_1 \times T_2))\), where \(\delta (q, q', a) = (\delta_{1} (q, a), \delta_{2}(q', a))\). Each state of \(A\) is a pair of states of \(A_1, A_2\).
Then \(A\) accepts a word iff the run with the word visits \((T_1 \times Q_2) \cup (Q_1 \times T_2)\) infinitely many times, which is equivalent to visiting \(T_1\) infinitely often, or visiting \(T_2\) infinitely often, or visiting both infinitely often. This means that the word is in \(L_1 \cup L_2\). Thus, \(L(A) = L_1 \cup L_2\).
2.1.3. Intersection of DBWs
DBW languages are closed under intersection. For any two DBWs, there is another DBW that recognize the intersection of languages of the two DBWs.
Let \(A_1, A_2\) be two automata and \(L_1 = L(A_1), L_2 = L(A_2)\). The tuples of \(A_1, A_2\) use the same notation as above.
\(L_1 \cap L_2\) consists of the words that visit both target sets infinitely many times, which is equivalent to alternating between both target sets infinitely many times (before switching to the other target set, can visit the same target set multiple times).
Consider two copies of the “joint” automata \(A_1 \times A_2\) \(A = (\Sigma, Q_1 \times Q_2 \times \{ L, R \}, (q_{01}, q_{02}) \times \{ L\}, \delta, T)\). We want to modify the transitions such that once the run reaches a target state in one copy, it switches to the other copt and continue the transition, so that it cannot visits target states in the same copy consecutively. We define the target set to be \(T = Q_1 \times T_2 \times \{ R \}\) and \(\delta\) by:
\begin{align*} \delta(q_1, q_2, L, a) = \begin{cases} (\delta_{1}(q_1, a), \delta_{2}(q_2, a), L), & \text{if } q_1 \notin T_1\\ (\delta_{1}(q_1, a), \delta_{2}(q_2, a), R), & \text{if } q_1 \in T_1\\ \end{cases}\\ \delta(q_1, q_2, R, a) = \begin{cases} (\delta_{1}(q_1, a), \delta_{2}(q_2, a), R), & \text{if } q_2 \notin T_2\\ (\delta_{1}(q_1, a), \delta_{2}(q_2, a), L), & \text{if } q_2 \in T_2\\ \end{cases}\\ \end{align*}A run in \(A\) visits \(Q_1 \times T_2 \times \{ R \}\) infinitely often iff it visits \(Q_1 \times T_2 \times \{ L \}\) infinitely often: Once it visits \(Q_1 \times T_2 \times \{ R \}\), it switches to \(Q_1 \times Q_2 \times \{ L \}\), and visits \(Q_1 \times T_2 \times \{ L \}\) zero or more times until it visits \(T_1 \times Q_2 \times \{ L \}\). vice versa.
2.1.4. Union of NBWs.
\(\omega\)-regular languages are closed under union. For any two NBWs, there is an NBW that recognize the union of languages of the two NBWs.
Let \(A_1 = (\Sigma, Q_1, Q_{01}, \delta_{1}, T_1)\) and \(A_2 = (\Sigma, Q_2, Q_{02}, \delta_{2}, T_2)\) and \(L_1, L_2\) be their languages, resp. We define \(A = (\Sigma, Q_1 \times \{ 1 \} \cup Q_2 \times \{ 2 \}, Q_{01} \times \{ 1 \} \cup Q_{02} \times \{ 2 \}, \delta_{1} \cup \delta_{2}, T_1 \times \{ 1 \} \cup T_2 \times \{ 2 \})\), where \((\delta_{1} \cup \delta_{2})((q, 1), a) = \delta_{1}(q, a), (\delta_{1} \cup \delta_{2})((q, 1), a) = \delta_{2}(q, a)\).
Basically, we keep two isolated components in \(A\). Then every accepting word in \(A_{i}\) corresponds to an accepting word in \(A\) starting from \(Q_{0i} \times \{ i \}\), and vice versa.
P.S.: Since DBW can have only one initial state, we cannot use this construction to prove the union of two DBWs.
2.1.5. Intersection of NBWs
\(\omega\)-regular languages are closed under intersection. For any two NBWs, there is an NBW that recognize the intersection of languages of the two NBWs.
The same proof as DBW works. The initial set becomes \(Q_1 \times Q_2 \times \{ L \}\). The definition for \(\delta\) becomes \(\delta(q_1, q_2, L, a) = \delta_{1}(q_1, a) \times \delta_{2}(q_2, a) \times \{ L \}\) if \(q_1 \notin T_1\), etc.
2.1.6. NBW Complement of DBW
For any DBW, there is an NBW that recognize the complement of the language of the DBW.
Let \(A = (\Sigma, Q, q_0, \delta, T)\) be a DBW. Intuitively, in a complement NBW \(B\) with the “same” (not exactly) set of states as \(A\), the accepting words should never see \(T\) after finitely many steps.
We define \(B = (\Sigma, Q', Q_0, \delta', T')\) as follows: \(Q' = (Q \times \{ 1 \}) \cup ((Q \setminus T) \times \{ 2 \})\), i.e., \(Q\) plus an extra copy of \(Q \setminus T\). \(Q_0 = \{ (q_0, 1) \}\). \(T' = (Q \setminus T) \times \{ 2 \}\). \(\delta'(q, 1, a) = \{\delta(q, a)\} \times \{ 1, 2 \}\), \(\delta'(q, 2, a) = (\{ \delta(q, a) \} \times \{ 2 \}) \cap T'\).
The accepting words of \(B\) are not accepted by \(A\): They visit \(T'\) infinitely many times, and will never visit \(T \times \{ 1 \}\) (corresponds to \(T\) in \(A\)) once entering \(T'\).
Conversely, the accepting words of \(A\) are not accepted by \(B\): To visit \(T\) (\(T \times \{ 1 \}\) in \(B\)) infinitely often, they cannot ever enter \(T'\).
Remark: This method is not applicable for finding NBW complement of NBW. In the nondeterministic setting, an accepting words may have one run that visits \(T \times \{ 1 \}\) infinitely often and another run that visits \(T \times \{ 2 \}\) infinitely often.
2.1.7. Emptiness of DBW/NBW
Given a DBW/NBW \(A\) with \(n\) states, decide whether \(L(A) = \emptyset\).
\(L(A) \neq \emptyset\) iff there exists an accepting run of \(A\) with an infinite word: Any valid run of \(A\) corresponds to a unique word, so the problem is equivalent to deciding whether \(A\) has an accepting run.
We can find a corresponding Buchi-game for emptiness problem: Let \(T\) be the set of accepting states in \(A\). We call the graph \((V, E)\) defined below the underlying graph of \(A\): \(V = Q\), and \((q_1, q_2) \in E\) iff \(\exists a \in \Sigma, q_2 \in \delta(q_1, a)\) (since we only care about the existence of an accepting run, not the characters in the run).
Define a single-player game \((V, V_1, V_2, E)\), where \(V_1 = V\) and \(V_2 = \emptyset\), with objective \(Buchi(T)\). Then \(L(A) \neq \emptyset\) iff there exists an outcome starting from an initial vertex \(\in Buchi(T)\), which is equivalent to \(Q_0 \cap Win_{1}(Buchi(T)) \neq \emptyset\).
A run corresponds to an outcome, and an accepting run, which visits \(T\) infinitely often, corresponds to a winning outcome starting from an initial vertex in the game.
Since the outcome is solely controlled by player 1, the condition is equivalent to \(Q_0 \cap Win_{1}(Buchi(T)) \neq \emptyset\).
Thus, this is solvable using the algorithm for finding winning set of Buchi game in \(O(n ^2)\) or \(O(n m)\) time.
- Linear-time algorithm
Consider the underlying game graph. Since the there are finitely many vertices, a run visits \(T\) infinitely often iff it visits a particular vertex in \(T\) infinitely often. Furthermore, this is equivalent to that there (1) there is a cycle containing a vertex in \(T\), (2) the cycle is reachable from the initial vertices.
Consider the strongly connected components of the graph. Condition (1) is equivalent to that an accepting state is contained by some non-transitional SCC, which is a SCC that is not a single vertex without a self-loop, i.e., a SCC that either is a single vertex with a self-loop or has at least two vertices.
The algorithm:
- Find all reachable vertices: Linear time.
- Find all SCCs: Linear time (tarjan).
- Check if a SCC contains an accepting state and is reachable: Linear time.
Overall, it is solvable in linear time \(O(n + m)\).
2.1.8. Universality Problem of DBW
The dual of emptiness.
Given a DBW \(A\), decide whether \(L(A) = \Sigma ^{\omega}\).
For a DBW, every word has a unique run and vice versa. Thus, \(L(A) = \Sigma ^{\omega}\) iff every run of \(A\) is accepting.
We have a corresponding coBuchi game for universality problem: Let \(T\) be the set of accepting states in \(A\). Define a game with the underlying graph of \(A\) as in the emptiness problem with objective \(coBuchi(T)\). Then, every run is accepting iff every path starting from an initial vertex is in \(Buchi(T)\), i.e., \(Q_0 \cap Win_{1}(coBuchi(T)) = \emptyset\).
Thus, the problem is solvable using the algorithm for find winning set of coBuchi game in \(O(n m)\) or \(O(n ^2)\).
- Linear-time algorithm
\(L(A) = \Sigma ^{\omega}\) iff every reachable cycle in the graph contains an accepting state.
Otherwise, there is a path that repeats a cycle containing no accepting state infinitely many times, and hence does not visit \(T\) infinitely many.
Every cycle contains an accepting state iff, after the removal of all accepting vertices, no cycle exists: This can be checked easily.
The algorithm:
- Remove all the unreachable vertices: Linear time.
- Remove all the accepting vertices: Linear time.
- Check whether there is a cycle in the remaining graph: Linear time.
Overall, it is solvable in linear time \(O(n + m)\).
2.1.9. Universality Problem of NBW
Non-universality of NBW is NP-hard.
Given a (undirected) graph \(G = (V, E)\), is it possible to color the vertices in \(G\) with 3 colors such that no two adjacent vertices have the same color?
We provide a reduction from 3-coloring, which is a classic NP-complete problem.
Given a (undirected) graph \(G = (V, E)\), let \(\Sigma = V \times \{ r, g, b \}\). We create the following NBWs:
The first NBW \(A\) is defined to accept all words that, when ignoring the colors, are not valid paths in \(G\). That is, a word \((v_1, c_1), (v_2, c_2), (v_3, c_3), \dots \) is accepting iff \(\rho = \langle v_1, v_2, v_3, \dots \rangle\) is an invalid path in \(G\).
\(A = (\Sigma, V \cup \{ \bot, q_0 \}, \{ q_0 \}, \delta, \{ \bot \})\) with Buchi condition, where:
\begin{align*} \delta(q_0, (v, c)) = v, \delta(u, (v, c)) = \begin{cases} v, & \text{if } (u, v) \in E\\ \bot, & \text{if } (u, v) \notin E \end{cases}, \delta(\bot, (v, c)) = \bot. \end{align*}A word is accepted by \(A\) iff the run ever transits through \((u, (v, c))\) for some \((u, v) \notin E\). Thus, the path associated with every accepting word contains an edge that is not in \(E\), and hence is invalid.
The second NBW \(B\) is defined to accept all words in which there is a vertex that appears with two different colors.
\(B = (\Sigma, A \cup \{ q_0 \}, \{ q_0 \}, \delta, B\) with Buchi condition, where \(A = \{ a_{v, c_1, c_2} | v \in V, c_1, c_2 \in \{ r, g, b \}, c_1 \neq c_2 \}\), \(B = \{ b_{v, c_1, c_2} | v \in V, c_1, c_2 \in \{ r, g, b \}, c_1 \neq c_2 \}\), and
\begin{align*} q_0 \in \delta(q_0, *), \forall c_1, c_2 \in \{ r, g, b \}, c_1 \neq c_2: &a_{v, c_1, c_2} \in \delta(q_0, (v, c_1)), \\ & a_{v, c_1, c_2} \in \delta(a_{v, c_1, c_2}, *),\\ & b_{v, c_1, c_2} \in \delta(a_{v, c_1, c_2}, (v, c_2)), \\ & b_{v, c_1, c_2} \in \delta(b_{v, c_1, c_2}, *). \end{align*}An accepting word is of the form \(\dots (v, c_1) \dots (v, c_2) \dots \).
The third NBW \(C\) is defined to accept all words that do not contain all edges of the graph. It is rather complicated to define \(C\) in expression, so we only show a subpart of it: The initial vertex \(Q_0\) includes \(q_{u,v}\) for all undirected edges \((u, v) \in E\). The subpart for an edge \((u, v) \in E\) is:
which accpets all the words that at least miss the edge \((u, v)\) (in either direction).
The fourth NBW \(D\) is defined to accepts all the words that have the same color twice in a row.
- The NBW \(E = A \cup B \cup C \cup D\) (\(L(E) = L(A) \cup L(B) \cup L(C) \cup L(D)\)).
We claim that \(E\) is universal iff \(G\) is not 3-colorable, i.e., \(E\) is not universal iff \(G\) is 3-colorable.
Only if side: \(E\) does not accept a word iff the word (a) is a valid path in \(G\), (b) assigns a unique color to each vertex, (c) visits all edges of \(G\), and (d) does not have the same color in a row. This is equivalent to that the word represent a valid 3-coloring of the graph.
If side: If \(G\) has a valid 3-coloring, then any infinite path that visits all edges together is an infinite word that is not accepted by \(E\).
Unless P=NP, there is no polynomial-time complementation of NBW.
Otherwise, we can run this polynomial-time complementation, and apply the (polynomial) emptiness algorithm to the complement to solve the universality in polynomial time.
2.1.10. Complementation NBW
Given a NBW \(A\), find an NBW \(B\) such that \(L(B) = \Sigma ^{\omega} \setminus L(A)\).
If we color each edge of a 6-vertex graph with one red and blue, then there must be a monochrome triangle.
Vertex 1 must have three edges of the same color, say blue. Consider the three vertices connected with 1 by blue edges. There are two cases: (1) At least two of them are connected by a blue edge, in which a blue triangle is formed. (2) All of them are connected by red edges, in which a red triangle is formed.
Consider a complete infinite graph \(G = (V, E)\) where every edge is colored by one of \(c\) colors. There is an infinite monochrome clique (complete subgraph induced by some vertices) in \(G\).
Let \(a_1 \in V\) be an arbitrary vertex. Since there are finitely many colors, there is a color \(c_1\) such that \(a_1\) has infinitely many neighbours with edge of color \(c_1\). Let the set of these neighbours be \(V_1\).
Consider the infinite graph \(G[V_1] = (V_1, V_1 \times V_1)\). For the same reason, there exists a vertex \(a_2\) and a color \(c_2\) with the same properties. Continuing this process forever, we get three infinite sequences \(a_1, a_2, \dots \), \(c_1, c_2, \dots \), \(V_1, V_2, \dots \).
Thus, there is a color \(c'\) that appears infinitely many times in \(c_1, c_2, \dots \). Let \(V' = \{ a_{i} | c_{i} = c' \}\). Clearly, \(V'\) (\(G[V']\)) is an infinite monochrome clique.
Given an NBW \(A\), we define an equivalence relaion over all non-empty finite words as follows: For \(v, w \in \Sigma^{+}\), we say \(v \sim w\) if
- For every pair of states \(q, q' \in Q\), there exists a run of \(A\) from \(q\) to \(q'\) over \(v\) iff there exists a run from \(q\) to \(q'\) over \(w\).
- For every pair of states \(q, q' \in Q\), there exists a run of \(A\) from \(q\) to \(q'\) over \(v\) that visits \(T\) iff there exists a run from \(q\) to \(q'\) over \(w\) that visits \(T\).
Define a function \(f_{v}: Q \to 2 ^{Q} \times 2 ^{Q}\) for each vertex \(v\) that maps \(q\) to \(\{ q' | q' \text{ is reachable using } v \}\) and \(\{ q' | q' \text{ is target-reachable using } v\}\). Then \(v \sim w\) iff \(f_{v} \equiv f_{w}\). Let \(L_{f}\) be the equivalence class of function \(f\), i.e., \(\{ v | f \equiv f_{v} \}\). Since we have finitely many such functions, we have finitely many equivalence classes.
Every \(L_{f}\) is regular (recognized by some NFA).
We can find an NFA that recognizes exactly \(L_{f}\):
- For every pair of states \(q, q' \in Q\), create an NFA \(C_{p,q'}\) that accepts all words \(v \in \Sigma ^{+}\) such that there is a run of \(A\) over \(v\) from \(q\) to \(q'\). We can take \(C_{p,q'}\) to be the same as \(A\) except that the initial state is \(q\) and the accepting state is \(q'\). Note that \(C_{p, q'}\) is non-deterministic, so the word it accepts may have other runs.
- For every pair of states \(q, q' \in Q\), create an NFA \(D_{p,q'}\) that accepts all words \(v \in \Sigma ^{+}\) such that there is a run of \(A\) over \(v\) from \(q\) to \(q'\) passing through \(T\). \(D_{p, q'}\) could just be the intersection of \(C_{p, q'}\) and an NFA that is the same as \(A\) except that the initial state is \(q\) and the set of accepting states is \(T\).
- Since any NFA has an NFA complement, there are \(C_{q, q'}^{-}\) that accepts all words that does not have a run from \(q\) to \(q'\) and \(D_{q, q'}^{-}\) that accepts all words that does not have a run from \(q\) to \(q'\) passing through \(T\).
- Let \(B\) the NFA that accepts all finite words. For \(q \in Q\), if \(f(q) = (Q_1, Q_2)\), then \[ B := B \cap \left( \bigcap _{q' \in Q_1} C_{q, q'} \right) \cap \left( \bigcap _{q' \notin Q_1} C_{q, q'}^{-} \right) \cap \left( \bigcap _{q' \in Q_2} D_{q, q'} \right) \cap \left( \bigcap _{q' \notin Q_1} D_{q, q'}^{-} \right). \] \(B\) is the NFA that recognizes \(L_{f}\).
For every infinite word \(w \in \Sigma ^{\omega}\), there is a decomposition \(w \in L_{f} (L_{g})^{\omega}\), where \(L_{f}, L_{g}\) are two equivalence classes of finite words. That is, \(w\) must be the concatenation of some finite word in \(L_{f}\) and infinitely many finite words in \(L_{g}\).
Let \(w = w_1 w_2 \dots \) be any infinite word, where each \(w_{i}\) is a symbol. We define \(w[i .. j) = w_{i} w_{i+1} \dots w_{j-1}\). Consider the infinite complete graph \(G(\mathbb{N} , \mathbb{N} \times \mathbb{N} )\). We view equivalence classes as colors, and color the edge \(\{ i,j \}\) with the (unique) \(L_{f}\) that contains \(w[i .. j)\).
By the Ramsey theorem, there is a color \(L_{g}\) such that there is an infinite monochrome clique \(i_0 < i_1 < \dots \) in which edges are all colored \(L_{g}\). Particularly, \(\{ i_0, i_1 \}, \{ i_1, i_2 \}, \dots \) all have color \(L_{g}\). Thus, \(w\) can be decomposed as \(w[1.. i_0) w[i_0 .. i_1) w[i_1 .. i_2) \dots \), implying that \(w \in L_{f} (L_{g})^{\omega}\), where \(L_{f}\) is the class containing \(w[1.. i_0)\).
Let \(L_{f}\) and \(L_{g}\) be equivalence classes. Either \(L(A) \cap L_{f} (L_{g})^{\omega} = \emptyset\) or \(L(A) \supseteq L_{f} (L_{g}) ^{\omega}\).
Let \(w \in L_{f} (L_{g}) ^{\omega}\), \(w = w_1 w_2 w_3 \dots \) where \(w_1 \in L_{f}\) and \(w_2, w_3, \dots \in L_{g}\) are finite words. Suppose \(w \in L(A)\), then by the definition of equivalence class, we can replace \(w_{i}\) by any word in the same class without affecting the times the run visits \(T\). Thus, the altered infinite words should also be \(\in L(A)\).
\(\omega\)-regular languages are closed under complementation. Any NBW has an NBW complement.
There are finitely many \(L_{f}\), so there are finitely many sets \(L_{f} (L_{g}) ^{\omega}\).
We have an NBW for every \(L_{g} ^{\omega}\): Take the NFA for \(L_{g}\). For each accepting state, create edges that the initial states have. The initial states and accepting states for the NBW are the same as the NFA.
We have an NBW for every \(L_{f} (L_{g}) ^{\omega}\): Take the NBW for \(L_{g} ^{\omega}\) and the NFA for \(L_{f}\). For each accepting state of the NFA, create edges that the initial states of the NBW have. The initial states of the resulting NBW are the intial states of the NFA, and the accepting states of the resulting NBW are the accepting states of the NBW for \(L_{g} ^{\omega}\).
Then take the union of NBWs of all \(L_{f} (L_{g}) ^{\omega}\) that does not intersect with \(L(A))\). Since every infinite word is in some \(L_{f} (L_{g}) ^{\omega}\), all the words in \(L(A) ^{c}\) are included.
2.1.11. Containment Problem
Given two DBW/NBW \(A\) and \(B\), decide whether \(L(A) \subseteq L(B)\).
Note that \(L(A) \subseteq L(B) \iff L(A) \cap L(B) ^{c} = \emptyset \iff L(A) \cap L(B ^{c}) = \emptyset\). If we can find the complement NBW \(B ^{c}\) of \(B\) (such that \(L(B ^{c}) = L(B) ^{c}\)), find the intersection automaton, and then answer the emptiness problem.
2.2. Parity Automata
A Parity Automaton is an Automaton on Infinite words with Parity acceptance condition: Let \(p: Q \to \{0, ..., d\}\) be a priority function, a run \(\varrho\) of the automaton is accepting if it satisfies the parity condition, i.e. \(\liminf(p(\varrho_{i}))\) is even.
We abbreviate Deterministic Parity Automaton to DPW, and the nondeterministic one to NPW.

