COMP 5712 Introduction to Combinatorial Optimization
1. Introduction
1.1. What is combinatorial optimization
\textbf{Combinatorial}: Study of finite discrete structure, e.g., graph.
Combinatorial \textbf{optimization problem}:
E.g., the input is a weighted graph. Problems can be
- Shortest path: find the shortest path between two vertices. \(\implies \) Polynomial-time Dijkstra’s algorithm
- Minimum spanning tree: find a spanning tree (connected and acyclic) of minimum cost. \(\implies \) Polynomial-time Prim’s or Kruskal’s algorithm.
- Traveling salesman problem (TSP): find the shortest closed path that visit each node exactly once. The total number of cycles in a complete graph is approximately \(n!\). \(\implies \) Currently no polynomial-time algorithm. It is NP-complete.
Common features:
- Each instance (input) of the problem is associated with a set of \textbf{finite} and \textbf{feasible solutions} (can be enumerated by bruteforce, e.g. ``any spanning tree’’ for MST, ``any cycle visiting each node exactly once’’ for TSP).
- Each feasible solution is associated with a number, called the ``objective function value’’. Typically the feasible solution is described in a concise manner rather than being implicitly listed.
- The goal is to develop an algorithm that finds the feasible solution that minimizes/maximizes the objective function value.
The problem whose answer is either yes or no.
The examples above are not decision problems themselves, but have some closely associated decision version. E.g.,
- ``Given a weighted graph \(G\) and a number \(k\), does \(G\) have a path between the two nodes with distance at most \(k\)?’’ for the shortest path problem;
- ``Given a completed weighted graph \(G\) and a number \(k\), does \(G\) have a TSP tour with distance at most \(k\)?’’ for TSP.
Optimization problems are harder than their corresponding decision problem: If we have the optimimal solution, we can solve the decision version immediately by comparing the solution with \(k\).
On the other hand, if we have an polynomial-time solution for the decision problem, we can also solve the optimization version in polynomial time. E.g., for MST, use binary search to try different value of \(k\). Note that enumerating from \(1\) to \(w\) (the largest possible weight) is exponential. Because in the worst case, edge weights can be \(w, 1, 1, 1, \dots \), so the input is at least of \(\log w\) bits, so \(w\) is exponential to the input length \(\log w\). \textbf{TODO} remove the edge safely.
Therefore, the optimization problem and the decision version are \textbf{equivalent up to polynomial time}.
the end of lecture 1 (7 Feb)
1.2. P and NP
Here are the informal but intuitive definitions of the complexity classes P and NP.
The class of \textbf{decision problems} that can be solved (solution exists) in polynomial time.
P.S.: from now on, whenever we some a problem is in some complexity class that consists only of decision problems, it means the decision version of that problem is in the class.
We don’t know whether TSP belongs to P, but it is believed that it does not. TSP is NP-complete.
The class of decision problems that there is (exists) a YES-certificate. More explicitly, for any YES-instance (input whose answer is YES), there exists a short proof/certificate that convince you the answer is YES (``short proof’’ means that its size is polynomial to the input size and can be check in polynomial time).
- the definition does not specify the condition on the time to find the proof.
E.g., TSP is in NP: for any YES-instance, the certificate can be some TSP tour with distance at most \(k\). Vertifying this tour is indeed of length \(\leq k\) (hence confirm that the answer is YES) can be done in polynomial time.
P is a subset of NP
Just take the YES-certificate as an empty string, then the checking process just ignore the certificate and solve the problem using the polynomial-time algorithm by itself.
A problem \(\Pi\) is said to be NP-complete if
- It belongs to NP
- There exists a polynomial-time reduction from any other NP problem to \(\Pi\). (polynomial-time reduction from \(\Pi_1\) to \(\Pi_2\) means that the reduction itself is polynomial-time. Therefore, if \(\Pi_2\) can be solved in polynomial time then \(\Pi_1\) can be reduced to it and be solved in polynomial time too.)
Problems in NP-complete are equivalent up to polynomial time: ``any other NP problem’’ can be another NP-complete problem.
As long as one NP-complete problem is shown to be P, then all NP problems are P. They are the hardest NP problems.
Do there exist NO-certificates for NP problems?
E.g., for TSP, having a NO-certificate means that there is a short proof that \(G\) have no TSP tour with distance at most \(k\). An obvious proof is to check every possible TSP tour, which is certainly not short.
We have no answer to whether NP problems have a NO-certificate, but the general belief is that the answer is no.
YES-certificate and NO-certificate are asymmetric.
Only the second condition of NP-complete.
- NP-hard problems can be optimization problems.
2. Steiner Tree Problem
Reference book: Lecture 2 of Luca Trevisan - Lecture Notes - 2011 Stanford cs261
2.1. Metric Steiner Tree Problem
Given a set \(X = R \cup S\) of points, where \(R\) is the set of required points and \(S\) is the set of optional/Steiner points, and a symmetric distance function \(d : X \times X \to \mathbb{R} _{\geq 0}\) (undirected complete graph). The goal is to find a minimum cost tree in \(G\) that contains all nodes in \(R\) and possibly some in \(S\).
This is very similar to MST, and the key difference lies in vertices required to span.
Restricted to the case in which \(d\) satisfies the triangle inequality, i.e., \(\forall u, v, w, d(u, v) \leq d(u, w) + d(w, v)\).
A distance function that is symmetric and satisfies the triangle inequality is called a semi-metric (to be a metric, \(d(x, y) = 0 \iff x=y\))
The decision versions of these problems are NP-complete.
The following approximation algorithm is a \(2\)-approximation:
- Construct a subgraph induced by \(R\).
- Return the MST of \(R\) in the subgraph.
Consider the optimal Steiner tree of cost \(OPT\).
We double the edges in the tree. Then all the nodes have even degrees. Therefore, the graph have Eulerian tours. An Eulerian tour can be derived by running a DFS starting from an arbitrary node, at each node:
- Go to its neighbours that are not visited.
- Go back to its predecessor only if there is none
This Eulerian tour is of length exactly \(2 OPT\).
Now we construct a spanning tree of \(R\) in the tour: We record the order of nodes in \(R\) in which they firstly present in the tour \(r_1 \to r_2 \to \dots \to r_{|R|}\). Then paths on the tour \((r_1, \dots , r_2)\), \((r_2, \dots , r_3)\), … , \((r_{|R|}, \dots , r_1)\) comprise a partition of the tour, of total length \(2 OPT\). And the path \((r_1, r_2, \dots , r_{|R|})\) (edges connecting adjacent nodes exist) (drop \((r_{|R|}, r_1)\)) is a shortcut of these paths by the triangle inequality, of length at most \(2 OPT\) (a path is also a tree).
Therefore, the minimum spanning tree, which is smaller than this one, is of length at most \(2 OPT\).
Illustration:
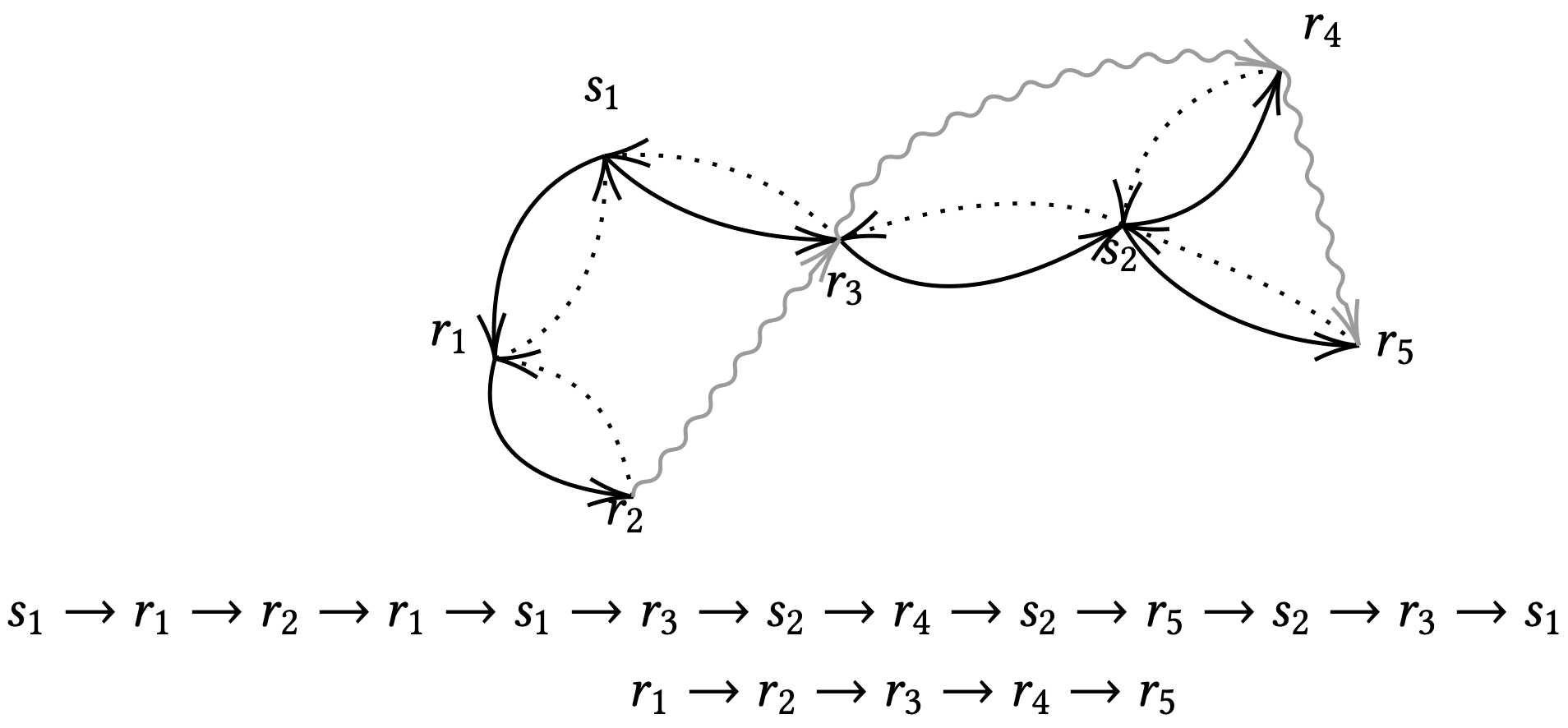
the end of lecture 2 (9 Feb)
The ratio \(2\) is tight for this algorithm because there are instances in which the ratio can be arbitrarily close to \(2\):
\(S = \{ v_0 \}\) and \(R = \{ v_1, \dots , v_{n} \}\). \(d(v_0, v_i) = 1\) for \(i = 1, \dots , n\) and \(d(v_i, v_j) = 2\) for all \(1 \leq i < j \leq n\). The optimal Steiner tree has \(v_0\) as the center and all required nodes connected to \(v_0\), so \(OPT = n\). However, the approx. algo. output a path of \(R\) in which each edge is of distance \(2\), so the total cost is \(2(n-1)\). Thus, the ratio is \( 2(n-1) / n\).
For any desired ratio less than \(2\), we can find sufficiently large \(n\) such that the actual ratio is greater than it. So \(2\) is tight.
The best approx. ratio known so far is \(1.39\).
And the hardness result is that, unless \(P = NP\), it is impossible to achieve approx. ratio better than \(96 /95\). That means that, if we can achieve a ratio smaller than that, it implies \(P = NP\). That is, finding a ratio better than that is a NP-hard problem.
The goal is either to find smaller approx. ratio, or to find larger lower bound of the ratio.
2.2. General Steiner Tree Problem
(There is a common reduction from the general problem to the metric one such that, ) For every \(c \geq 1\), if there is a polynomial time \(c\)-approximate algorithm for Metric Steiner Tree, then there is a polynomial time \(c\)-approximate algorithm for General Steiner Tree.
The details are stated in the proof.
\textbf{The reduction} basically constructs a new graph that satisfies the triangle inequality: Let the original graph be \(G\), we construct \(G'\) with a distance function \(d'\) in the following way: For any two points \(x\) and \(y\) in \(G\), let \(d'(x, y)\) be the length of the shortest path from \(x\) to \(y\) in \(G\). Then \(d'\) satisfies the triangle inequality: For every three points \(x, y, z\), the shorest path from \(x\) to \(y\) plus the one from \(y\) to \(z\) is \textbf{some} path from \(x\) to \(z\), so its length cannot be shortest than the length of the \textbf{shortest} path from \(x\) to \(z\), i.e., \(d'(x, z) \leq d'(x, y) + d'(y, z)\).
Then, we run the \(c\)-approximate algo. on \(G'\). Let the cost of the output solution be \(SOL(G')\), then \(SOL(G') \leq c \cdot OPT(G')\).
Next, we convert the solution to a solution to the original problem. We replace each edge \((x, y)\) in the solution by the shortest path from \(x\) to \(y\) in \(G\). At this stage, the total cost does not change. However, the converted solution may have duplicate edges and cycles, so we simply remove the duplicate edges, and take a MST of the remaining graph as the final solution. Clearly, the MST is a valid Steiner tree. It only removes edges, so \(MST \leq SOL(G') \leq c \cdot OPT(G')\).
3. Metric Traveling Salesman Problem
Find the shortest closed path that visit each node exactly once.
Given a complete weighted graph \(G\) with nonnegative weights satisfying the triangle inequality, find the cheapest cycle that reaches all points exactly once.
3.1. \(2\)-approximate Algorithm
The following approximation algorithm is a \(2\)-approximation:
- Construct a MST
- Find a \textbf{twice-around tour} of the MST. (i.e. an Eulerian tour extracted from the doubled-edge graph)
- \textbf{Shortcut} a TSP tour from the twice-around tour. (i.e., directly jump to the next unseen point, such edge exists because of the complete graph).
By dropping an edge on an optimal TSP tour, we get \textbf{a} spanning path of the graph. So its cost must be \(\geq \) the MST. Therefore, \(OPT \geq MST\).
Similar to before, the shortcut TSP tour has cost \(SOL \leq 2 \cdot MST \leq 2 \cdot OPT\).
The general steps of constructing an approximate ratio are the following:
- Find a lower bound of \(OPT\). (In this case, \(MST \leq OPT\))
- Use the lower bound to extract a solution. In this process, the cost of the solution becomes worse than the lower bound, but they have some relationship. (In this case, \(SOL \leq 2 \cdot MST\))
- Finally, derive the relationship between \(OPT\) and \(SOL\) with the lower bound as the medium.
3.2. \(\star\) \(3/2\)-approximate Algorithm
We want to find a Eulerian tour. And the Eulerian tour exists \textbf{iff} all the vertices have even degrees. Since some nodes are already of even degree, we could consider adding fewer edges.
Also notice that the number of vertices of odd degree must be even. So we could divide these odd vertices into pairs and add an edge between each pair of vertices.
the end of lecture 3 (14 Feb)
Given a graph \(G = (V, E)\), a subset \(M \subseteq E\) is a matching if no pair of edges in \(M\) share common endpoints.
A matching is called perfect if it covers all nodes in \(V\).
A min-weight perfect matching is a perfect matching that achieve the minimum possible total weight.
Given a complete graph \(G\) with an even number of nodes, it is possible to compute a min-weight perfect matching in polynomial time.
\textbf{The following is a polynomial $3/2$-approximate algorithm}:
- Construct a MST
- Let \(S\) be the set of nodes of even degree in the MST, and \(G_{S}\) be the subgraph of \(G\) induced by \(S\). Find the min-weight perfect matching \(M\) in \(G_S\).
- Find an Eulerian tour in the union of the MST and \(M\).
- Shortcut the Eulerian tour to form a TSP tour.
The theorem follows immediately if the following lemma is true. (Note that we do not need to double the edges in \(MST \cup M\), so the TSP tour \(\leq \) the Eulerian tour \(= MST + M\))
The weight of the min-weight perfect matching in \(G_S\) is no greater than \( \frac{1}{2} OPT\), where \(OPT\) is the weight of the optimal TSP in \(G\).
Consider the optimal TSP tour. We shortcut it (vertex set \(V\)) to form a tour (cycle) of \(S\) (\(\subseteq V\)). The cycle has weight \(C \leq OPT\).
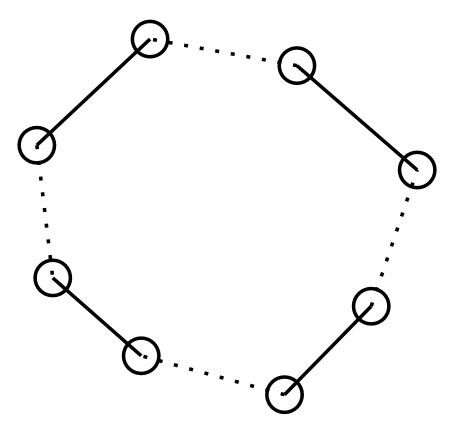
Then we partition this cycle into two perfect matching of \(S\) by putting every two adjacent edges to different matchings. The sum of the weights of these two matchings is equal to \(C\), so the smaller weight among them must be \(\leq \frac{1}{2} C \leq \frac{1}{2} OPT\).
The min-weight perfect matching is smaller than or equal to this matching, so its weight is also \(\leq \frac{1}{2} OPT\).
4. Linear Programming
The term ``programming’’ means ``planning’’.
A linear program comprises
- A linear function of serveral vairables \(x_1, x_2, \dots , x_n\) we want to optimize (maximize / minimize), called the \textbf{objective function}.
- A number of linear inequalities of these variables, called constraints. The inequal signs can be either \(\geq \) or \(\leq \), but one can easily negative the coefficients to flip and unify the sign.
- The nonnegativity constraint, i.e. all variables should be nonnegative.
The goal is to optimize the objective function under these constraints.
Formally, a LP can be written as
\begin{align*} \text{maximize} & \quad \sum_{j=1}^{n} c_j x_j \\ \text{subject to} & \quad \sum_{j=1}^{n} a_{ij} x_j \leq b_i, \quad i = 1, \dots , m\\ & \quad x_j \geq 0, \quad j = 1, \dots , n \end{align*}For minimization versions, we only need to negative the objective function and constraints accordingly.
The region satisfying all the constraints.
In the 2-dimensional case, the constaints are half plains, and the objective function at some fixed value is a straight line.
A region such that for any two points in it the line segment connecting them is also (entirely) in the region.
It can be easily shown that the intersection of two convex region is also a convex region.
Since the a (high-dimensional) half plain is a convex region, the feasible region which is the intersection of all constraints is also a convex region.
The Integer Linear Programming (ILP) (with an additional constraint that all \(x_i\) are integers) is NP-complete. So any NP problem can be reduced to an ILP problem.
For a maximization (minimization) problem, we want a good approximation, i.e., a tight upper bound (lower bound) of maximal (minimal) solution. So we can first convert it to an ILP problem, and then relax the integer constraint. The maximal (minimal) solution or the upper bound (lower bound) of the resulting LP problem will certainly be an upper bound (lower bound) of the original ILP problem (can achieve better results due to less constraints).
4.1. Matrix Representation
Let
\begin{align*} \vec{x} = \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}, \qquad \vec{c} = \begin{pmatrix} c_1 \\ \vdots \\ c_n \end{pmatrix}, \qquad \mat{A}_{i, j} = a_{ij}, \qquad \vec{b} = \begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix} \end{align*}be the column vector of all variables, the column vector of coefficients of the objective function, the \(n \times m\) matrix of coefficients of the left-hand sides of the constraints, and the column vector of right-hand sides of the constraints, respectively. Then the LP can be written as
\begin{equation} \label{eq:lp-mat} \begin{split} \text{maximize} & \quad \vec{c} ^{\intercal} \vec{x} \\ \text{subject to} & \quad \mat{A} \vec{x} \leq \vec{b} \\ & \quad \vec{x} \geq \vec{0} \end{split} \end{equation}where \(\leq ,\geq \) is the entry-wise \(\leq ,\geq \).
- Any \(\vec{x} \in \mathbb{R} ^n\) satisfying all the constraints of LP is called a \textbf{feasible solution}.
- Any \(\vec{x ^{*}} \in \mathbb{R} ^n\) that achieve the maximum/minimum possible value of \(\vec{c} ^T \vec{x}\) among all feasible solutions is called an \textbf{optimal solution}.
- An LP is \textbf{infeasible} if its feasible region is \(\emptyset\).
- An LP is \textbf{unbounded} if the \textbf{objective function} can attain arbitrary large (small) value for maximization (minimizaation) problem.
the end of lecture 4 (16 Feb)
Geometric explanation of \(\vec{c} ^{\intercal} \vec{x}\): All \(\vec{x}\) satisfying \(\vec{c} ^{\intercal} \vec{x} = \vec{c} \cdot \vec{x} = k\) for some fixed value \(k\) are on a line/hyper plane orthogonal to \(\vec{c}\).
4.2. LP Duality
Suppose we have a maximization problem LP, called \textbf{primal LP} (similar for minimization problem). To construct an upper bound on the objective, we try to find a linear combination of the contraints with positive coefficients, which form a inequality of a linear combination of the variable \(\vec{x}\), in which the coefficients of \(\vec{x}\) are at least \(\vec{c} ^{T}\):
\begin{align*} y_i \geq 0, i = 1, \dots , m, \qquad \sum_{i=1}^{m} y_i \cdot a_{ij} \geq c_j, j = 1, \dots , n. \end{align*}Then, the inequality gives an upper bound on the objective.
\begin{equation} \label{eq:1} \sum_j ^n c_j x_j \leq \sum_{j=1}^{n} \left( \sum_{i=1}^{m} y_i a_{ij} \right) x_j = \sum_{i=1}^{m} y_i \sum_{j=1}^{n} a_{ij} x_j \leq \sum_{i=1}^{m} y_i b_i \end{equation}The dual LP has the multipliers of the constraints as its variables, trying to minimize the resulting upper bound:
\begin{multicols}{2} \begin{equation} \begin{split} \text{minimize} & \quad \sum_{i=1}^{m} b_i y_i \\ \text{subject to} & \quad \sum_{i=1}^{m} a_{ij} y_i \geq c_j, \quad j \in [n]\\ & \quad y_i \geq 0, \quad i \in [m] \end{split} \end{equation}\break \begin{equation} \begin{split} \text{minimize} & \quad \vec{b} ^{\intercal} \vec{y} (\vec{y} ^{\intercal} \vec{b})\\ \text{subject to} & \quad \mat{A}^{\intercal} \vec{y} \geq \vec{c} (\vec{y} ^{\intercal} \mat{A} \geq \vec{c} ^{\intercal})\\ & \quad \vec{y} \geq \vec{0} \end{split} \end{equation} \end{multicols}Conversely, the primal LP is also the dual of the dual LP.
The definition naturally implies the following result:
If \(x_i\) and \(y_i\) are an arbitrary pair of feasible solutions for the primal and dual LP, respectively, then
\begin{align*} \sum_{i=1}^{m} c_j x_i \leq \sum_{i=1} ^m b_i y_i \end{align*}Given a primal LP
\begin{align*} \text{maximize} & \quad \vec{c} ^{\intercal} \vec{x} \\ \text{subject to} & \quad \mat{A} \vec{x} \leq \vec{b} \\ & \quad \vec{x} \geq \vec{0} \end{align*}, the dual LP is
\begin{align*} \text{minimize} & \quad \vec{b} ^{\intercal} \vec{y} (\vec{y} ^{\intercal} \vec{b})\\ \text{subject to} & \quad \mat{A}^{\intercal} \vec{y} \geq \vec{c} (\vec{y} ^{\intercal} \mat{A} \geq \vec{c} ^{\intercal})\\ & \quad \vec{y} \geq \vec{0} \end{align*}Note that \(\vec{y} ^{\intercal} \mat{A}\) is just the linear combination of the (LHS of) inequalities in the primal LP.
If \(\vec{x}\) and \(\vec{y}\) are feasible solutions for the primal and dual LP, respectively, then
\begin{align*} \vec{c} ^{\intercal} \vec{x} \leq \vec{b} ^{\intercal} \vec{y} \end{align*}By \(\mat{A} \vec{x} \leq \vec{b}\) and \(\vec{y} \geq \vec{0}\), we have \(\vec{y} ^{\intercal} \mat{A} \vec{x} \leq \vec{y} ^{\intercal} \vec{b}\). By \(\vec{y} ^{\intercal} \mat{A} \geq \vec{c} ^{\intercal}\) and \(\vec{x} \geq 0\), we have \(\vec{y} ^{\intercal} \mat{A} \vec{x} \geq \vec{c} ^{\intercal} \vec{x}\). Therefore, \(\vec{c} ^{\intercal} \vec{x} \leq \vec{b} ^{\intercal} \vec{y}\).
If the primal LP is unbounded, then the dual LP is infeasible.
If either the primal LP or the dual LP is feasible and bounded, then so is the other and the optimal objective function value of both LPs are the same.
We assume that the primal LP is feasible and bounded.
The solution \(\vec{x}\) that achieves the maximum value must be at some intersection vertex of two constraints. Let us denote it by \(\vec{x}^{*}\), and the two constraints by \(\vec{a_i} \cdot \vec{x} \leq b_i\) and \(\vec{a_j} \cdot \vec{x} \leq b_j\), where \(\vec{a_i}\) and \(\vec{a_j}\)are the \(i\)-th and \(j\)-th rows of \(\mat{A}\) orthogonal to the constraint lines. These two are satisfied with equalities, i.e.,
\begin{align*} \vec{a_i} \cdot \vec{x} ^{*} = b_{i}, \quad \vec{a_j} \cdot \vec{x} ^{*} = b_{j} \end{align*}Since the primal LP is bounded, the two constraint lines must form a triangle with some line orthogonal to \(\vec{c}\), so \(\theta_i + \theta_j < \pi\). Therefore, \(\vec{c}\) lies in the corner of \(\vec{a_i}\) and \(\vec{a_j}\), meaning that \(\vec{c}\) can be expressed as
\begin{align*} \vec{c} = y_i ^{*} \vec{a_i} + y_j ^{*} \vec{a_j}, \quad y_i ^{*}, y_j ^{*} \geq 0 \end{align*}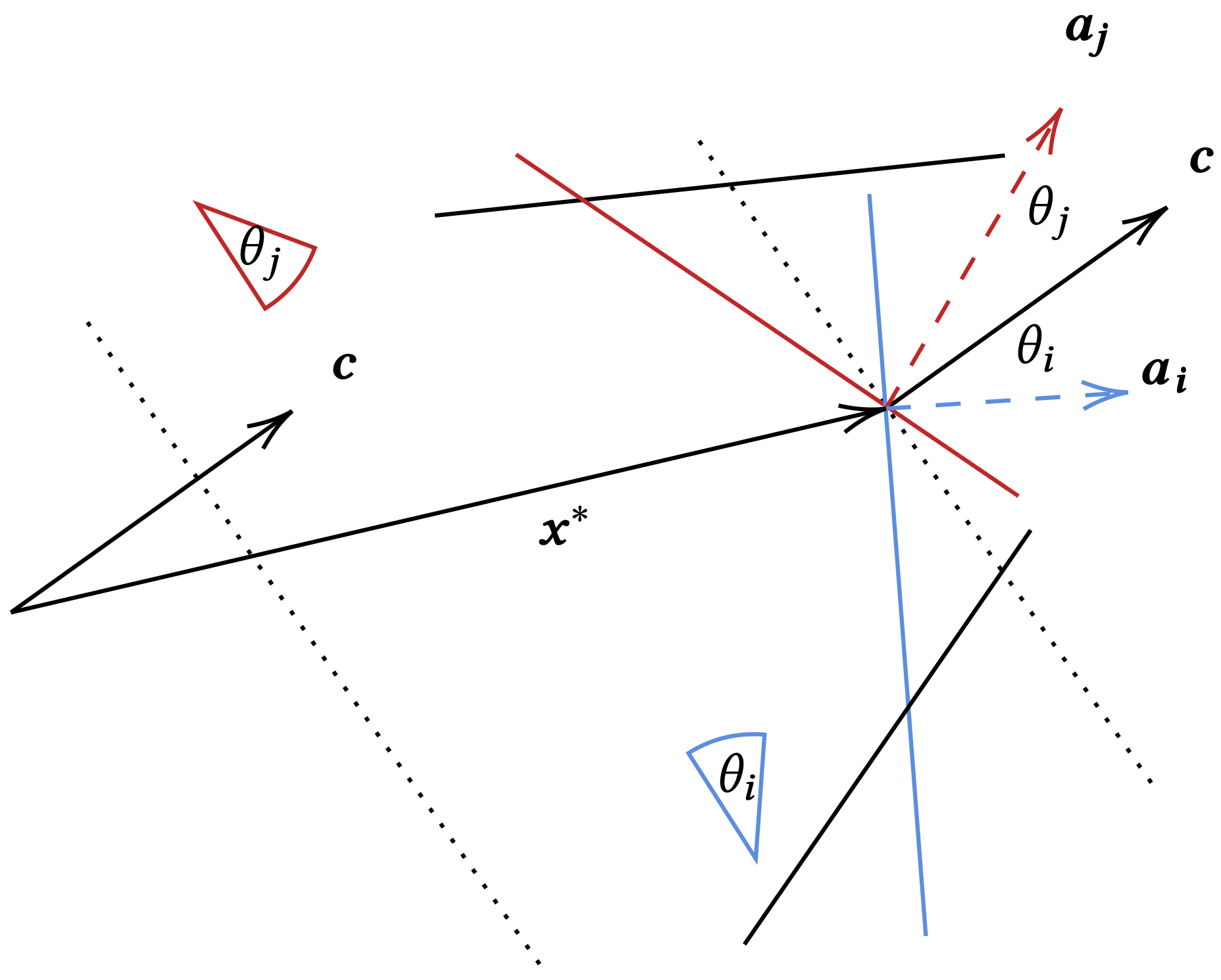
As the notation \(y ^{*}\) indicates, \(y ^{*}\)’s are the multipliers of the constraints of the primal LP, and hence \(\vec{y}^{*}\) is a solution for the dual LP. More rigorously, we let \(y ^{*}_k = 0\) for \(k \neq i, j\) and check that \(\mat{A} ^{\intercal}\vec{y}^{*} = \vec{c} \geq \vec{c}\) and \(\vec{y}^{*} \geq \vec{0}\). \(\vec{y}^{*}\) is indeed a feasible solution for the dual.
The objective function value of the dual is
\begin{align*} \vec{b} ^{\intercal} \vec{y} ^{*} = b_i y ^{*}_i + b_j y ^{*}_j \end{align*}and the optimal value of the primal is
\begin{align*} \vec{c} ^{\intercal} \vec{x} ^{*} = y ^{*}_i \vec{a_i} \cdot \vec{x}^{*} + y ^{*}_k \vec{a_j} \cdot \vec{x}^{*} = b_i y ^{*}_i + b_j y ^{*}_j \end{align*}They are equal. Therefore, by the weak duality theorem, their optimal values are the same.
Let \(n\) be the number of constraints plus the number of variables, and \(L\) be the number of input bits (input numbers should be \(\in \mathbb{Q} \), where each can be represented by two integers. If they are \(\in \mathbb{R} \), that is too complicated).
Then LP can be solved in time polynomial to \(n\) and \(L\).
5. Minimum Weighted Vertex Cover
- \(\Pi\): optimization problem (min or max).
- \(I\): instance of \(\Pi\).
- \(OPT_{\Pi}(I)\): the objective function value of the optimal solution to instance \(I\), sometimes abbreviated to \(OPT(I)\) if \(\Pi\) is clear.
- \(OPT_{ILP}(I) = OPT_{\Pi}(I)\): the objective function value of the equivalent ILP.
- \(OPT_{LP}(I)\): the objective function value of the relaxed LP, sometimes denoted by \(OPT_{f}(I)\) meaning ``fractional’’.
Given an undirected graph \(G = (V, E)\) with a positive weight \(w_v\) associated with each vertex \(v\). The goal is to find a \(V' \subseteq V\) that covers all the edges and minimizes the total weight \(\sum_{v \in V'} w_v \).
This is known to be a NP-hard problem.
An equivalent ILP is
\begin{align*} \text{minimize} & \quad \sum_{v \in V} w_v x_v \\ \text{subject to} & \quad x_u + x_v \geq 1, \forall e = (u, v) \in E\\ & \quad x_v \in \{0, 1\}, x_v = 1 \text{ means } v \in V' \end{align*}Then we want to relax this ILP to a LP to get a lower bound of the minimal solution. An obvious relaxation is let \(x_v \in [0, 1]\). However, fractional value of \(x_v\) does not make sense. We shall show that rounding \(x_v\) in some way can give a valid solution for the original problem. Before that, we propose a simpler relaxation:
The LP is the same as the ILP but the integrality constraint is relaxed to \(0 \leq x_{v} \leq 1\). It turns out that it can be further replaced by \(x_v \geq 0\).
\(0 \leq x_{v} \leq 1\): If the optimal solution for the relaxed LP has some \(x_v > 1\), then changing it to \(1\)
- will not break \(x_u + x_v \geq 1\), because \(1 \geq 1\) and \(x_u \geq 0\),
- and can reduce the objective function value because \(w_v > 0\).
So by doing this we can obtain a better solution. Therefore, in the optimal solution every \(x_v \leq 1\).
The following rounding method leads to a \(2\)-approximation: Let \(x_{v} ^{*}\) be the optimal solution for the LP. Round \(x_v ^{*} \geq \frac{1}{2}\) to \(1\) and \(x_v ^{*} < \frac{1}{2}\) to \(0\).
In other words, we take \(S = \{ v \in V : x_{v} ^{*} \geq \frac{1}{2} \}\) as the output.
Validness: Every edge has at least one endpoint with corresponding \(x ^{*}\) value \(\geq \frac{1}{2}\), so after rounding this endpoint becomes \(1\) and meet the constraint.
Approximation ratio: Let the rounded solution be \(x_{v}'\) and objective function value of the rounded solution be \(SOL\). Since \(OPT_{LP} \leq OPT_{VC}\), it suffices to show \(SOL \leq 2 OPT_{LP}\): If \(x_v ^{*} \geq \frac{1}{2}\), then \(x_{v}' = 1 \leq 2 x_{v} ^{*}\). If \(x_{v} ^{*} < \frac{1}{2}\), then \(x_{v}' = 0 \leq 2 x_{v} ^{*}\). So
\begin{align*} SOL = \sum_{v \in V} x_{v}' \leq \sum_{v \in V} 2 x_{v}^{*} = 2 \sum_{v \in V} x_{v}^{*} = 2 \cdot OPT_{LP} \end{align*}the end of lecture 5 (23 Feb)
For a minimization problem \(\Pi\), the integrality gap for a LP relaxation for \(\Pi\) is
\begin{align*} \max_{I} \frac{OPT_{\Pi}(I)}{OPT_{LP}(I)} \end{align*}
For a maximization problem, it is
\begin{align*} \max_{I} \frac{OPT_{LP}(I)}{OPT_{\Pi}(I)} \end{align*}- To lower bound the integrality gap, we just need to find an instance \(I\).
- To upper bound it, we investigate the (worst-case) approximation ratio. Because for any instance \(I\), we always have \(\frac{SOL(I)}{OPT_{LP}(I)} \geq \frac{OPT_{\Pi}(I)}{OPT_{LP}(I)}\). And the approximation ratio is just the worst \(\frac{SOL(I)}{OPT_{LP}(I)}\).
\textbf{Lower bound}: when the input is a complete graph \(K_{n}\). Then the optimal fractional solution is \(x_{v} = \frac{1}{2}\) for each vertex, while the optimal integral solution is picking all but one vertex. The rounded solution will be picking every vertex. So
\begin{align*} \frac{OPT_{VC}(K_{n})}{OPT_{LP}(K_{n})} = \frac{2(n-1)}{n} = 2 - \frac{2}{n} \end{align*}\textbf{(Tight) upper bound}: We have shown that \(\frac{SOL(I)}{OPT_{ILP}(I)} \leq 2\) for any \(I\). Next, we find an instance with the ratio exactly \(=2\): When the input is a complete bipartite graph \(K_{n, n}\), the optimal fractional solution is still \(x_{v} = \frac{1}{2}\) for each vertex, while the integral solution is picking one side of vertices. The rounded solution is still picking all the vertices. So
\begin{align*} \frac{SOL(K_{n, n})}{OPT_{VC}(K_{n, n})} = \frac{2n}{n} = 2 \end{align*}Thus, the approximation ratio is tight. In addition, the ratio \(2\) is an tight upper bound of the integrality gap.
In conclusion, the gap is in \([2 - \frac{2}{n}, 2]\) for any \(n \in \mathbb{N} \).
Best approximation ratio for VC: \(2 - \Theta(1 /\sqrt{\log_{n}})\)
Open question: Find a approximation ratio of \(2 - \delta\) for some fixed \(\delta > 0\), or prove that it is NP-hard.
Hardness result: Unless \(P = NP\), there is no approximation better than \(1.36\).
the end of lecture 6 (28 Feb)
5.1. The dual of the LP relaxation
By the Weak Duality theorem, the objective function value of any feasible solution to the dual LP is a lower bound on the optimal value of the primal LP.
The dual LP of the primal LP is
\begin{align*} \text{maximize} & \quad \sum_{e \in E} y_{e}\\ \text{subject to} & \quad \sum_{e: e \text{ is indicent on } v} y_{e} \leq w_{v}, \quad \forall v \in V\\ & \quad y_{e} \geq 0, \quad \forall e \in E \end{align*}Using natural language, the problem can be described as follows: Assign a nonnegative \textbf{charge} to each edge such that the weight of every vertex is enough to \textbf{pay} for the sum of charges of edges that are incident on the vertex. Find the maximal total charge over all edges.
Will construct a feasible solution \(\vec{y}\) to the dual LP and a feasible solution \(\vec{x}\) to the \textbf{I}LP (i.e., integral \(\vec{x}\)) in parallel. We call a vertex \(v\) tight if the the sum of charges is equal to its weight.
The algorithm is:
- Initiate \(\vec{x}, \vec{y} \gets \vec{0}\).
- For each edge \(e = (u, v) \in E\) (in any order)
- Raise the charge \(y_{e}\) as much as possible until at least one of its endpoint is tight.
- Choose all of its tight endpoints to the vertex cover, i.e., if \(u\) is tight then set \(x_{u} \gets 1\), and if \(v\) is tight then set \(x_{v} \gets 1\).
- Output the \(\vec{x}\) and \(\vec{y}\) as the solutions to the ILP and dual LP, respectively, and \(S = \{ v | x_{v} = 1 \}\) as the vertex cover.
\(S\) is a \(2\)-approximation.
We can show the correctness and approximation ratio using the Weak Duality theorem or from scratch.
Validness (every edge is covered): We raise the charge of every edge until it has an endpoints selected into the VC. Thus, every edge is covered.
Approximation ratio: \(S\) and \(\vec{y}\) are the VC and the solution to the dual outputed by the above algorithm, respectively.
\begin{align*} w(S) = \sum_{v \in S} w_{v} &= \sum_{v \in S} \sum_{e \text{ incident on } v} y_{e}\\ &= \sum_{e \in E} y_{e} \times (\text{Number of its endpoints that are tight})\\ &\leq 2 \sum_{e \in E} y_{e} \leq 2 OPT_{VC} \tag{the second ineq. by WD} \end{align*}Validness: the same.
Approximation ratio: Let \(C\) be an arbitrary VC, and \(\vec{y}\) be the solution given by the above algorithm.
As proved before, \(w(S) \leq 2 \sum_{e \in E} y_{e}\). It suffices to show \(\sum_{e \in E} y_{e} \leq w(C ^{*})\) for an optimal VC \(C ^{*}\).
\begin{align*} w(C ^{*}) = \sum_{v \in C ^{*}} w_{v} &\geq \sum_{v \in C ^{*}} \sum_{e \text{ incident on } v} y_{e} \tag{by the constraint}\\ &= \sum_{e \in E} y_{e} \times (\text{Number of its endpoints that are in } C ^{*})\\ &\geq \sum_{e \in E} y_{e} \tag{\(C\) covers each edge at least once} \end{align*}the end of lecture 7 (02 Mar)
5.2. Unweighted
A maximum matching is a matching with the largest possible number of edges. A maximal matching, however, is a matching that cannot include any more edges. A maximal matching does not necessarily contain the largest number of edges.
Finding a maximal matching can be done in polynomial time: Incrementally add (any) edges until no more edges can be added.
A \(2\)-approximate algorithm for the minimum unweighted vertex cover problem is
- Find a maximal matching.
- Take all endpoints of the matching as the vertex cover.
\textbf{Validness}: If some edge is not covered, then neither of its endpoints is selected into the VC. This is impossible.
\textbf{By direct combinatorial argument}: Any VC must cover the maximal matching \(M\). Since edges in \(M\) do not share common endpoints, any VC must use at least \(|M|\) vertices. Therefore the output has cost \(2 |M| \leq 2 \cdot OPT\).
\textbf{By the weak duality theorem}: A feasible solution to the dual is setting the charge of every edge in \(M\) to be \(1\), resulting in the total cost \(|M|\). By the WDT, \(|M|\) is a lower bound on the cost the optimal solution to the primal (VC).
6. Set Cover Problem
Given a finite \textbf{universal} set \(U\) and a collection of subsets of \(U\): \(S_1, \dots , S_{n}\) such that \(\cup _{i=1}^{n} S_{i} = U\), each associated with weight \(w_{i}\).
A set cover is a collection of these sets whose union is \(U\). The goal is to find a SC of the smallest cost. I.e., find a \(I \subseteq \{ 1, 2, \dots , n \}\) such that \(\cup _{i \in I} S_{i} = U\) and \(\sum_{i \in I} w_{i}\) is minimized.
THe VC problem can be reduced to a SC problem: Take \(U\) as the set of all the edges \(E\), and \(S_{i}\) as the set of edges incident to the vertex \(i\).
The equivalent ILP to the SC problem is
\begin{align*} \text{minimize} & \quad \sum_{i=1}^{n} w_{i} x_{i}\\ \text{subject to} & \quad \sum_{i: u \in S_{i}} x_{i} \geq 1, \quad \forall u \in U\\ & \quad x_{i} \in \{ 0, 1 \}, \quad i = 1, 2, \dots , n \end{align*}6.1. A LP Relaxation and A Randomized Approximation
A LP relaxation is changing \(x_{i} \in \{ 0, 1 \}\) to \(x_{i} \geq 0\). The proof is exactly the same as for the VC problem. In addition, \(OPT_{LP} \leq OPT_{SC}\).
If we attempt to apply the deterministic rounding method for the VC, i.e., threshold \( \frac{1}{2}\), then we will find it does not give an valid SC in general. For instance, some \(i\) is included in all the sets, then the corresponding contraint will be \(x_1 + \dots + x_{n} \geq 1\). In the optimal solution, \(x_{i}\) can be as small as \( \frac{1}{n}\), so all of them will be rounded down to zero.
Let \(x_{i}^{*}\) be the optimal solution for the LP-relaxation. Pick \(S_{i}\) to the SC with probability \(x_{i} ^{*}\).
Let \(C\) be the solution. Then the expected cost of \(C\) is at most \(OPT_{SC}\), and each element is covered with probability at least \(1 - \frac{1}{e}\).
\textbf{Expected cost}:
\begin{align*} \E [cost(C)] &= \sum_{i=1}^{n} w_{i} \cdot \prob (S_{i} \text{ is selected}) \tag{by linearity}\\ &= \sum_{i=1}^{n} w_{i} x_{i}^{*} \leq OPT_{SC} \end{align*}\textbf{The probability that \(u \in U\) is covered}:
It is easier to compute the probability that \(u\) is NOT covered: Assume \(u\) is covered by \(k\) sets, \(S_{i_1}, \dots , S_{i_{k}}\). Then
\begin{align*} \prob (u \notin C) &= \prod_{i=1}^{k} \prob (S_{i} \text{ is not selected})\\ &= (1 - x_{i_1}^{*}) \cdots (1 - x_{i_{k}}^{*})\\ &\leq \left( 1 - \frac{1}{k} \right)^{k} \tag{\(x_{i_1} + \dots + x_{i_{k}} \geq 1\)}\\ &\leq \frac{1}{e} \end{align*}Alternatively, by \(1 - x \leq e ^{-x}\), we have \((1 - x_{i_1}^{*}) \cdots (1 - x_{i_{k}}^{*}) \leq e ^{-x_{i_1} ^{*} - \dots - x_{i_{k}} ^{*}} \leq e ^{-1}\).
So the probability that \(u\) IS covered is \(\geq 1 - \frac{1}{e}\).
We say something is true with high probability (w.h.p.) if the probability is
\begin{align*} \geq 1 - \frac{1}{\text{poly}(\text{input})} \end{align*}We cannot say \(C\) is a valid SC w.h.p.: Though not exactly following the definition, we can see
\begin{align*} \E(\text{Number of elements covered}) \geq |U| \cdot \left( 1 - \frac{1}{e} \right) \end{align*}is not a good bound, because is only shows that a constant fraction of elements are covered.
Given the optimal solution for the LP-relaxation \(x_{i}^{*}\), the following algorithm gives a valid SC w.h.p., whose cost is expected to be a \((c \ln |U|)\)-approximation, and runs in deterministic polynomial-time:
- Independently pick \((c \ln |U|)\) collections (\(C_{i}\)’s) using the above randomized rounding method.
- Take the union of them to form the solution \(C'\).
collections by \(t\) (t for times).
\textbf{Probability that \(C'\) is valid}: Since it takes the union,
\begin{align*} \prob (u \notin C') = \prob (u \notin C_{i} \forall i) = \prod_{i} \prob (u \notin C_{i}) \leq \left( \frac{1}{e} \right) ^{t} \end{align*}When \(t = c \ln |U|\), \(\prob (u \notin C') = \frac{1}{|U| ^{c}}\).
Then
\begin{align*} \prob (C' \text{ is not valid}) &= \prob (u_1 \notin C' \lor \dots \lor u_{|U|} \notin C')\\ &\leq \sum_{i=1}^{|U|} \prob (u_i \notin C') \tag{\textbf{union bound}}\\ &\leq \frac{1}{e ^{t}} \cdot |U| \end{align*}When \(t = c \ln |U|\), \(\prob (C' \text{ is not valid}) \leq \frac{1}{|U| ^{c-1}}\). We can say \(C'\) is valid w.h.p.
\textbf{Expected cost}:
\begin{align*} \E [cost(C')] \leq \sum \E[cost(C)] \leq t \cdot OPT \end{align*}when \(t = c \ln |U|\), it is \(\leq (c \ln |U|) OPT\).
\textbf{Running time}: polynomial.
the end of lecture 8 (07 Mar)
If \(X\) is a nonnegative r.v. and \(t > 0\), then
\begin{align*} \prob (X \geq t) \leq \frac{\E X}{t} \end{align*}\(\E X \geq t \prob (X \geq t) + 0 \prob (X < t)\)
Given the optimal solution for the LP-relaxation \(x_{i}^{*}\), in expected polynomial time, the following algorithm is guaranteed to give a valid \(O(\ln |U|)\)-approximation of the cost of the optimal SC:
Repeatedly
- Run the algorithm in Thm~1.
- Check the cost and validness
until the solution is valid and the cost is \(O(\ln |U|) \cdot OPT_{LP}\).
- Output the solution.
Here we show for \(O(\ln |U|) = 4 \cdot c \ln |U|\), where the constant \(c\) is from Thm~1.
\textbf{Running time}:
Let \(C'\) be the solution derived in each iteration. We first get some constant bounds for the two ``bad things’’:
- Validness: \(\prob (C' \text{ is not valid}) \leq \frac{1}{|U| ^{c-1}} \leq \frac{1}{4}\) when \(|U| \geq 2\) and \(c > 3\).
- Cost too large: By the Markov’s inequality, \(\prob [cost(C') \geq 4 \cdot c \ln |U| OPT_{LP}] \leq \frac{\E cost(C')}{4 \cdot c \ln |U| OPT_{LP}} = \frac{1}{4}\).
Therefore, the probability that either of them happens is \(\prob [\text{cost too high} \lor \text{SC not valid}] \leq \frac{1}{2}\) (by the union bound). Then the probability that both of them pass the check is \(\prob (\text{terminate}) \geq \frac{1}{2}\). The # iterations follow the Geometric distribution, so
\begin{align*} \E (\text{Number of iters}) = \frac{1}{\prob (\text{terminate})} \leq 2 \end{align*}Since each iteration (including the checking) can be done polynomial, the overall running time is expected to by polynomial.
\textbf{Approximation ratio}: guaranteed to be \(t\). (In this case, \(t = 4 \cdot c \ln |U|\)).
Harndess result: If for some constant \(\epsilon > 0\), there is a polynomial-time \((1-\epsilon) \ln |U|\) approximation, then \(P = NP\).
6.2. \(\star\) The Dual of the Relaxation and A Greedy Algorithm
The dual of the (weighted SC) LP relaxation is
\begin{align*} \text{maximize} & \quad \sum_{u \in U} y_{u}\\ \text{subject to} & \quad \sum_{u: u \in S_{i}} y_{u} \leq w_{i}, \quad i = 1, \dots , n\\ & \quad y_{u} \geq 0, \quad \forall u \in U \end{align*}By analogy to the VC problem, we interpret \(y_{u}\) as the charge of the element \(u\).
We hope the set we choose to cost less and cover more. This reminds us to choose according to the ratio of # elements covered by the cost.
The following algorithm gives a \(O(\ln |U|)\) approximation:
- \(I \gets \emptyset\)
- While there is some element that has not been covered
- Let \(D\) be the set of uncovered elements.
- For every set \(S_{i}\), let the effectiveness \(e_{i} = \frac{|D \cap S_{i}|}{w_{i}}\).
- Let \(S_{i ^{*}}\) be a set with the highest effectiveness.
- Add \(i ^{*}\) to the index set \(I\).
- Return \(I\).
To prepare for the proof, we first define some notations:
- Let \(u_1, \dots , u_{m}\) be an enumeration of the elements in the order in which they are covered by the algorithm. (the order of elements covered at the same time does not matter)
- Let \(c_{j}\) be the effitiveness of the set that was picked at the step in which the algorithm covered \(u_{j}\) for the first time. \(c_{j}\) is the largest among all \(e_{i}\) at that stage.
- The reciprocal \(\frac{1}{e_{i}} = \frac{w_{i}}{|D \cap S_{i}|}\) represents the average cost to cover an element \(\in D \cap S_{i} \subseteq D\).
\(OPT_{SC} \geq \frac{m-j+1}{c_{j}}, \forall j \in \{ 1, 2, \dots , m \}\)
- \( \frac{1}{c_{j}}\) is the smallest to cover any uncovered element in \(D\).
The optimal solution covers \(D_{j}\), so it has cost at least \(|D_{j}| \cdot \frac{1}{c_{j}} \leq \frac{m-j+1}{c_{j}}\).
- Let \(D_{j}\) be the set of uncovered elements just before the step in which \(u_{j}\) is covered. Note that \(|D_{j}| \geq m-j+1\).
\(c_{j}\) is the largest # elements to be covered per unit of cost. The optimal solution covers \(D_{j}\). In the best case, every unit \(OPT_{SC}\) can cover \(c_{j}\) elements, so \(OPT_{SC} \cdot c_{j} \geq |D_{j}| \geq m-j+1\).
- Every set \(S_{i}\) of weight \(w_{i}\) cover at most \(c_{j} \cdot w_{i}\) elements.
Assign \(y_{u_1}, \dots , y_{u_{j-1}} = 0\), and \(y_{u_{j}}, \dots , y_{u_{m}} = \frac{1}{c_{j}}\). Check that for every set \(S_{i}\), \(\sum y_{u} = \frac{1}{c_{j}} \cdot |S_{i} \cap D_{j}| \leq \frac{1}{c_{j}} \cdot (c_{j} w_{i}) = w_{i}\).
The objective function value is \(|D_{j}| \cdot \frac{1}{c_{j}} \geq \frac{m-j+1}{c_{j}}\). By the weak duality theorem, this is a lower bound of \(OPT_{SC}\).
Let \(APX\) be the cost of the greedy solution. By the proposition above,
\begin{align*} APX &= \sum_{j=1}^{m} \frac{1}{c_{j}} \leq \sum_{j=1}^{m} \frac{OPT_{SC}}{m-j+1}\\ &= OPT_{SC} \sum_{j=1}^{m} \frac{1}{j} = OPT_{SC} [\ln m + o(1)] \end{align*}the end of lecture 9 (09 Mar)
7. Network flow
7.1. Definition
A flow network is a directed graph \(G = (V, E)\) with \(2\) special vertices source \(s\) and sink \(t\), in which each edge \(e\) is associated with a capacity \(c(e) \geq 0\).
A flow \(f\) is an assignment of values to edges such that the following constraints are satisfied
- Capacity constraint: \(\forall e \in E, f(e) \leq c(e)\)
- Flow conservation: \(\forall v \in V - \{ s, t \}, \sum_{u \in V} f(u, v) = \sum_{u \in V} f(v, u) \). There is no edges into \(s\) and no edges leaving \(t\).
The flow value of \(f\), denoted by \(|f|\), is defined as the total flow out of the source
\begin{align*} \sum_{v \in V} f(s, v) \end{align*}The goal is to find a flow of maximum flow value from \(s\) to \(t\).
A partition \((A, V - A)\) of the vertex set into two groups, such that \(s \in A\) and \(t \in V - A\). We may simply refer to this cut as cut \(A\).
The \textbf{capacity of a cut}, denoted by \(c(A)\), is \(c(A) = \sum_{u \in A, v \notin A} c(u, v)\).
Any cut gives an upper bound on any flow value. That is, \(|f| \leq c(A)\) for any \(f\) and \(A\).
Given a flow \(f\) and a cut \(A\), the net flow out of \(A\) is defined as the total flow out of \(A\) minus the total flow into \(A\). That is,
\begin{align*} f(A) := \sum_{a \in A, b \notin A} f(a, b) - \sum_{a \in A, b \notin A} f(b, a) \end{align*}Consider any flow \(f\) and any cut \(A\), \(|f| = f(A)\).
\(f(A)\) only involves flows across \(A\) and \(V - A\). To make use of the flow conservation, we consider completing all the flow out of and into \textit{nodes in \(A\)}.
Since flows within \(A\) are cancelled out,
\begin{align*} \sum_{a \in A} \left( \sum_{b \in V} f(a, b) - \sum_{b \in V} f(b, a) \right) = f(A) \end{align*}Since flow are conserved at all nodes \(\in A\) except \(s\),
\begin{align*} \sum_{a \in A} \left( \sum_{b \in V} f(a, b) - \sum_{b \in V} f(b, a) \right) = \sum_{b \in V} f(s, b) \end{align*}Thus, \(|f| = f(A)\).
the end of lecture 10 (14 Mar)
By Lemma~1, \(|f| = f(A)\). By the definition of \(f(A)\),
\begin{align*} f(A) \leq \sum_{a \in A, b \notin A} c(a, b) - \sum_{a \in A, b \notin A} 0 = c(A) \end{align*}Thus, \(|f| \leq c(A)\).
If we find some flow \(f\) and some cut \(A\) such that \(|f| = c(A)\), then \(f\) is the maximum flow and \(A\) is the minimum cut.
Given a flow \(f\), the residual network w.r.t \(f\) is a flow network with the same vertex set \(V\), same source and sink, with edges as follows:
- Forward edge: If \(f(u, v) < c(u, v)\), then insert edge \((u, v)\) with capacity \(c(u, v) - f(u, v)\).
- Backward edge: If \(f(u, v) > 0\), then insert \((v, u)\) with capacity \(f(u, v)\).
If we can pick a flow through the residual network, it can be easily check that this flow plus the existing flow in the original network is still a valid network. And such a (positive) flow augment the exisiting flow.
Repeatedly
- Find a simple path from \(s\) to \(t\) in the residual network, called an augmenting path.
- Find the minimum capacity \(\Delta\) of any edge on this path.
- Update the flow in the original network by pushing this extra flow \(\Delta\).
Until there is no augmenting path.
In case all the quantities are integral, the number of iterations is \(O(OPT)\).
The correctness follows from the max flow min cut theorem below. We first investigate the running time of this algorithm:
Consider the this network: \href{https://en.wikipedia.org/wiki/File:Ford-Fulkerson\_example\_0.svg}{wikipedia}
If the capacities are \(2 ^{100}\) except that the one in the middle is \(1\).
Then the worst case is to augment through the \(1\) edge every time. So it terminates after \(2 \cdot 2 ^{100}\) iterations, which is exponential to the input size.
the end of lecture 11 (16 Mar)
7.2. Max flow min cut theorem
The following 3 conditions are equivalent for a flow \(f\) in a network:
- There is a cut whose capacity equals \(|f|\).
- The flow \(f\) is optimal.
- There is no augmenting path for flow \(f\).
- [1 to 2] By weak duality (corollary before).
- [2 to 3] By contradiction. Suppose \(f\) is optimal but there is some augmenting path, then pushing this path will increase the flow value.
[\(\star\) 3 to 1] By construction. Let \(A\) be the set of vertices reachable from \(s\) in the residual network. Then, by definition, there is no edge (with positive capacity) from \(A\) to \(V - A\). This means that every edge \(e\) from \(A\) to \(V - A\) has flow \(f(e) = c(e)\) and every edge from \(V - A\) to \(A\) has flow \(0\). Thus,
\begin{align*} f(A) = \sum_{a \in A, b \notin A} c(a, b) - \sum_{a \in A, b \notin A} 0 = c(A) \end{align*}Since \(|f| = f(A)\), we get \(|f| = c(A)\).
- The max flow must exist: The objective function is bounded (e.g., the total capacity of edges leaving \(s\)) and there is a trivial feasible solution \(f(e) = 0 \forall e \in E\), so the optimal solution must exist.
- The theorem does not rely on the termination of the algorithm.
Checking \(f\) is optimal can be done in linear time.
By (3), that is to check the existense of augmenting paths: Run a BFS from \(s\) to \(t\) in the residual network. If \(t\) is reachable from \(s\), then the augmenting path exists.
By (2), that is to check whether the capacity of the constructed cut equals \(|f|\).
7.3. Fattest Augmenting Path Algorithm
Define the fatness of a path in a flow network to be the minimum capacity of the edges along the path.
The algorithm: At each iteration of Ford-Fulkerson method, choose the fattest augmenting path in the residual network.
This algorithm runs in polynomial time.
\textbf{TODO} There is a \(O(|E| \log |V|)\) algorithm to find the fattest augmenting path.
Given a flow network \((G = (V, E), s, t, c)\) and a flow \(f\) in the network. We can decomposite a flow \(f\) into \(f_1, \dots , f_{k}\) as follows:
- Find a simple path \(p_{i}\) from \(s\) to \(t\) in which every edge carries positive flow.
- Let \(f_{i}\) be the maximum flow through this path. Namely, \(|f_{i}| = \) the minimum flow on edges in \(p_{i}\).
- Subtract \(f_{i}\) from the flow \(f\). At least one edge (the smallest) becomes zero and is removed from the network.
- Repeat this process until the flow is fully decomposited.
The decomposition satisfies \(|f| = \sum_{i}^{k} |f_{i}|\) and \(k \leq O|E|\).
Since \(f_{i}\)’s are disjoint:
There is a path from \(s\) to \(t\) in which every edge has capacity \(\geq \frac{OPT}{|E|}\).
We always apply the lemma to the residual network: Let \(OPT_{res}\) be the optimal flow value in the residual network. Since the edges in the residual network is \(\leq 2|E|\) (forward and backward), the lemma says we can find a augmenting path of value \(\geq \frac{OPT_{res}}{2|E|}\).
Stage 1: The goal is to achieve a total flow value of \(OPT \sim \frac{OPT}{2}\). Thus, before reaching the goal, \(OPT_{res} \in [\frac{OPT}{2}, OPT]\) and the fattest augmenting path has value \(\geq \frac{OPT /2}{2 |E|} = \frac{OPT}{4|E|}\). Hence, at most \(2|E|\) iterations are needed to reach the goal.
State \(i\): The goal is to achieve a flow value \(OPT \sim \frac{OPT}{2 ^{i}}\). So \(OPT_{res} \leq \frac{OPT}{2 ^{i}}\), the fattest augmenting path has value \(\geq \frac{OPT}{2 ^{i+1}|E|}\), and the number of iterations needed is \(\leq 2|E|\).
Since \(OPT\) is integral, the algorithm terminates in \(O(\log |OPT)\) stages. In each stage, there are \(O(|E|)\) iterations, each costing polynomial time (\(|E| \log |V|\)). So the total running time is \(O(poly \cdot |E| \log |OPT|)\).
the end of lecture 12 (21 Mar)
We have argued that the fattest augmenting path has value \(\geq \frac{OPT_{res}}{2 |E|}\). For simplicity, we denote the \(OPT_{res}\) in the \(i\)-th iteration by \(res_{i}\). Since \(res_{i}\) equals \(res_{i-1}\) minus the value of the augmenting path, \(res_{i} \leq res_{i-1} \left( 1 - \frac{1}{2 |E|} \right)\).
By induction, this implies \(res_{i} \leq OPT \left( 1 - \frac{1}{2 |E|} \right) ^{i}\). Setting \(i = 2 |E| \log OPT\), we get \(res_{i} \leq OPT \cdot e ^{- \log OPT} = 1\). So the number of iterations is \(O(|E| \log |OPT|)\).
the end of lecture 13 (23 Mar)
7.4. Strongly Polynomial Time: Edmonds-Karp Algorithm
An algorithm runs in strongly polynomial time if, assuming unit time arithmetic operations (\(+, -\), etc.), the running time is polynomial in # numerical quantities given as input.
If the running time is polynomial but not in # numerical quantities (e.g., depends on the magnitude/bits of the input), then the algorithm is weakly polynomial time.
E.g., for the network flow problem, a strongly polynomial time algorithm is polynomial in \(|E|, |V|\), but a weakly polynomial time algorithm can be polynomial in \(|OPT|\) (which depends on the input bits).
E.g., the fattest path algorithm (\(O(|E| \log |V| \cdot |E| \log |OPT)\)) is weakly polynomial time.
E.g., for LP, no strongly polynomial time algorithm is known. The ellipsoid method and interior point method are both weakly polynomial time.
A specific implementation of the Fold-Fulkerson method. In each iteration, it finds an \(s\)-\(t\) path in the residual network with the fewest # edges (shortest length).
Finding a path with shortest length can be easily done using a BFS in polynomial time (\(O(|V| + |E|) = O(|E|)\)).
If, at a certain iteration, the shortest \(s\)-\(t\) path is of length \(l\), then at every subsequent iteration the length will be \(\geq l\).
Furthermore, after at most \(|E|\) iterations, the shortest length becomes \(\geq l + 1\).
The simple path can have length at most \(|V| - 1\). So it immediately follows from the theorem that the total number of iterations is \(O(|E| \cdot |V|)\), and so the total running time is \(O(|V| \cdot |E| ^2)\).
Consider the residual network after \(T\) iterations. Construct a BFS tree of the residual network starting at \(s\). We call \(V_0, V_1, \dots \) the vertices in the 0th, 1st layers etc. \(s\) is in \(V_0\) and \(t\) is in \(V_{l}\).
Note that a BFS tree has no downward edges that across more than \(1\) layers (no \((u, v)\) on the tree such that \(u \in V_{i}, v \in V_{j}, j - i > 1\)).
Suppose we pick a length-\(k\) path \(p\) from \(s\) to \(t\) in the \((T+1)\)-th iteration and push \(p\) to the flow in the original graph. At least one edges in \(p\) has been saturated and disappears in the BFS tree, while the opposite edges of every edge in \(p\) appears in the BFS tree.
Since this only adds edges from higher-numbered layer to lower-numbered ones, and every step on a path can advance at most by one layer, the shortest path from \(s\) to \(t\) is at least \(l\).
Furthermore, if all edges in length-\(l\) paths in the original BFS have been saturated and reversed, the shortest length becomes \(\geq l + 1\). Since each time we reverse at least one edge, this process takes at most \(|E|\) iterations.
7.5. Bipartite Graphs
A bipartite graph \(G = (V, E)\) with bipartition \((L, R)\) such that \(|L| = |R|\) has a perfect matching if and only if for every \(A \subseteq L\) we have \(|A| \leq |N(A)\).
\textbf{TODO}
\(C = (L - S) \cup (R \cap S)\) is a vertex cover.
8. Appendix
By \(1 + x \leq e ^{x}\) for \(x \in \mathbb{R} \), we have \(1 - \frac{1}{x} \leq e ^{-1 /x}\). Since \(t ^{x}\) is an increasing function of \(t\) on \([0, + \infty)\) for \(x \geq 1\), we take both sides to the power of \(x\) and get the result.